题目内容
11.已知函数f(x)=lnx-x-3.(Ⅰ)求函数f(x)的最大值;
(Ⅱ)求证:ln(22+1)+ln(32+1)+ln(42+1)+…ln(n2+1)<1+2lnn!(n≥2,n∈N*)
分析 (I)判断f(x)的单调性,从而计算f(x)的最大值;
(II)根据f(x)在(1,+∞)上单调递减可得f(x)<-4,化简得ln(x)<x-1,利用对数的运算性质计算ln(22+1)+ln(32+1)+ln(42+1)+…ln(n2+1)-2lnn!,根据f(x)的单调性化简,再使用不等式性质得出结论.
解答 解:(I)f′(x)=$\frac{1}{x}-1$,令f′(x)=0得x=1,
∴当0<x<1时,f′(x)>0,当x>1时,f′(x)<0,
∴f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
∴f(x)的最大值为f(1)=-4.
(II)证明:∵f(x)=lnx-x-3在(1,+∞)上单调递减,
∴f(x)<f(1)=-4,即lnx-x-3<-4,
∴lnx<x-1在(1,+∞)上恒成立,
∴ln($\frac{1}{{n}^{2}}$+1)<$\frac{1}{{n}^{2}}$,
∴ln(22+1)+ln(32+1)+ln(42+1)+…+ln(n2+1)-2lnn!
=ln$\frac{({2}^{2}+1)•({3}^{2}+1)•…•({n}^{2}+1)}{{n}^{2}•(n-1)^{2}•(n-3)^{2}•…•{2}^{2}}$
=ln[(1+$\frac{1}{{2}^{2}}$)(1+$\frac{1}{{3}^{2}}$)…(1+$\frac{1}{{n}^{2}}$)]
=ln(1+$\frac{1}{{2}^{2}}$)+ln(1+$\frac{1}{{3}^{2}}$)+…+ln(1+$\frac{1}{{n}^{2}}$)
<$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+$\frac{1}{{4}^{2}}$+…+$\frac{1}{{n}^{2}}$
<$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{n(n-1)}$
=1-$\frac{1}{2}+\frac{1}{2}-\frac{1}{3}$+…+$\frac{1}{n-1}-\frac{1}{n}$
=1-$\frac{1}{n}$<1.
点评 本题考查导数与函数单调性的关系,利用函数性质证明不等式,以及考查学生创造性的分析解决问题的能力,属于中档题.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案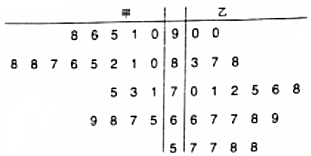
(1)现从乙班数学成绩不低于80分的同学中随机抽取两名同学,求至少有一名成绩为90分的同学被抽中的概率;
(2)学校规定:成绩不低于75分的为优秀.请填写下面的2×2表,并判断有多大把握认为“成绩优秀与教学方式有关”.
| 甲班 | 乙班 | 合计 | |
| 优秀 | 14 | 8 | 22 |
| 不优秀 | 6 | 12 | 18 |
| 合计 | 20 | 20 | 40 |
| P(x2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.79 | 10.828 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
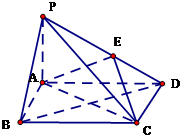 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.