题目内容
2.已知函数f(x)=x-alnx+b,a,b为实数.(Ⅰ)若曲线y=f(x)在点(1,f(1))处的切线方程为y=2x+3,求a,b的值;
(Ⅱ)若|f′(x)|<$\frac{3}{{x}^{2}}$对x∈[2,3]恒成立,求a的取值范围.
分析 (I)根据导数的几何意义可得f′(1)=2,f(1)=5,列方程组解出a,b即可;
(II)分离参数得出x-$\frac{3}{x}$<a<x+$\frac{3}{x}$,分别求出左侧函数的最大值和右侧函数的最小值即可得出a的范围.
解答 解:(I)f′(x)=1-$\frac{a}{x}$,
∵曲线y=f(x)在点(1,f(1))处的切线方程为y=2x+3,
∴f′(1)=2,f(1)=5,
∴$\left\{\begin{array}{l}{1-a=2}\\{1+b=5}\end{array}\right.$,解得a=-1,b=4.
(II)∵|f′(x)|<$\frac{3}{{x}^{2}}$对x∈[2,3]恒成立,即|1-$\frac{a}{x}$|<$\frac{3}{{x}^{2}}$对x∈[2,3]恒成立,
∴|x-a|<$\frac{3}{x}$对x∈[2,3]恒成立,
∴x-$\frac{3}{x}$<a<x+$\frac{3}{x}$对x∈[2,3]恒成立,
设g(x)=x-$\frac{3}{x}$,h(x)=x+$\frac{3}{x}$,x∈[2,3],
则g′(x)=1+$\frac{3}{{x}^{2}}$>0,h′(x)=1-$\frac{3}{{x}^{2}}$>0,
∴g(x)在[2,3]上是增函数,h(x)在[2,3]上是增函数,
∴gmax(x)=g(3)=2,hmin(x)=h(2)=$\frac{7}{2}$.
∴a的取值范围是[2,$\frac{7}{2}$].
点评 本题考查了导数的几何意义,导数与函数单调性的关系,函数最值的计算,属于中档题.

练习册系列答案
相关题目
13.已知圆C的方程为x2+y2=1,直线l的方程为x+y=2,过圆C上任意一点P作与l夹角为45°的直线交l于A,则|PA|的最小值为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\sqrt{2}-1$ | D. | $2-\sqrt{2}$ |
10.已知抛物线y2=4x的焦点为F,直线l过F且与抛物线交于A、B两点,若|AB|=5,则AB中点的横坐标为( )
| A. | $\frac{5}{2}$ | B. | 2 | C. | $\frac{3}{2}$ | D. | 1 |
7.已知长方体ABCD-A1B1C1D1中,AB=BC,AA1=2AB,E为AA1中点,则异面直线BE与CD1所形成角的余弦值为( )
| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{3\sqrt{10}}{10}$ | D. | $\frac{3}{5}$ |
14.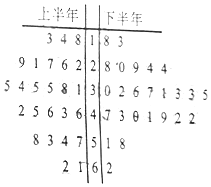 自贡某工厂于2016年下半年对生产工艺进行了改造(每半年为一个生产周期),从2016年一年的产品中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示(如图).已知每个生产周期内与其中位数误差在±5范围内(含±5)的产品为优质品,与中位数误差在±15范围内(含±15)的产品为合格品(不包括优质品),与中位数误差超过±15的产品为次品.企业生产一件优质品可获利润20元,生产一件合格品可获利润10元,生产一件次品要亏损10元
自贡某工厂于2016年下半年对生产工艺进行了改造(每半年为一个生产周期),从2016年一年的产品中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示(如图).已知每个生产周期内与其中位数误差在±5范围内(含±5)的产品为优质品,与中位数误差在±15范围内(含±15)的产品为合格品(不包括优质品),与中位数误差超过±15的产品为次品.企业生产一件优质品可获利润20元,生产一件合格品可获利润10元,生产一件次品要亏损10元
(Ⅰ)求该企业2016年一年生产一件产品的利润为10的概率;
(Ⅱ)是否有95%的把握认为“优质品与生产工艺改造有关”.
附:
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
 自贡某工厂于2016年下半年对生产工艺进行了改造(每半年为一个生产周期),从2016年一年的产品中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示(如图).已知每个生产周期内与其中位数误差在±5范围内(含±5)的产品为优质品,与中位数误差在±15范围内(含±15)的产品为合格品(不包括优质品),与中位数误差超过±15的产品为次品.企业生产一件优质品可获利润20元,生产一件合格品可获利润10元,生产一件次品要亏损10元
自贡某工厂于2016年下半年对生产工艺进行了改造(每半年为一个生产周期),从2016年一年的产品中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示(如图).已知每个生产周期内与其中位数误差在±5范围内(含±5)的产品为优质品,与中位数误差在±15范围内(含±15)的产品为合格品(不包括优质品),与中位数误差超过±15的产品为次品.企业生产一件优质品可获利润20元,生产一件合格品可获利润10元,生产一件次品要亏损10元(Ⅰ)求该企业2016年一年生产一件产品的利润为10的概率;
(Ⅱ)是否有95%的把握认为“优质品与生产工艺改造有关”.
附:
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |