��Ŀ����
1��ij��ѧ��ѧ��ʦ�ֱ������ֲ�ͬ��ѧ��ʽ����ѧ��ѧƽ���ֺ������ʶ���ͬ�ļס���������һ�°ࣨ������Ϊ20�ˣ����н�ѧ�������ѧ��ѧϰ���������ѧ��ѧϰ��ѧ�ڷ̶ܳȺ��Ծ��Զ�һ��������ͼ��ʾ��Ҷͼ�磮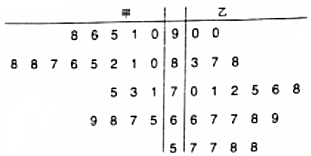
��1���ִ��Ұ���ѧ�ɼ�������80�ֵ�ͬѧ�������ȡ����ͬѧ����������һ���ɼ�Ϊ90�ֵ�ͬѧ�����еĸ��ʣ�
��2��ѧУ�涨���ɼ�������75�ֵ�Ϊ���㣮����д�����2��2�������ж��ж�������Ϊ���ɼ��������ѧ��ʽ�йء���
| �װ� | �Ұ� | �ϼ� | |
| ���� | 14 | 8 | 22 |
| ������ | 6 | 12 | 18 |
| �ϼ� | 20 | 20 | 40 |
| P��x2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.79 | 10.828 |
���� ��1��������Ұ���ѧ�ɼ�������80���������ɼ�Ϊ90�ֵ�ͬѧ�������������������û����¼��ĸ��������ùŵ���͵ĸ��ʹ�ʽ���㣻
��2�����ݾ�Ҷͼ�ֱ�����ס��Ұ�����������벻������������г����������������ָ����ʽ����K2�Ĺ۲�ֵ���Ƚ����ٽ�ֵ�Ĵ�С���жϳɼ��������ѧ��ʽ�йصĿɿ��Գ̶ȣ�
��� �⣺��1���Ұ���ѧ�ɼ�������80�ֵ�ͬѧ��5�������гɼ�Ϊ90�ֵ�ͬѧ��2����
��5��ͬѧ�г�ȡ2��������C52=10�ַ�����
����������һ��ͬѧ90�ֵij鷨��C22+C21C31=7�֣�
���������P=$\frac{7}{10}$��
��2��2��2��������
| �װ� | �Ұ� | �ϼ� | |
| ���� | 14 | 8 | 22 |
| ������ | 6 | 12 | 18 |
| �ϼ� | 20 | 20 | 40 |
��90%���ϵİ�����Ϊ�ɼ��������ѧ��ʽ�йأ�
���� ���⿼�����ɾ�Ҷͼ�������������������������������������ָ��K2�Ĺ۲�ֵ�������˹ŵ���͵ĸ��ʼ��㣬�ۺ���ǿ������Ҫϸ�ģ��ɹ�ʽ�������ָ��K2�Ĺ۲�ֵ���ɹ۲�ֵ�жϳɼ��������ѧ��ʽ�йصĿɿ��Գ̶��ǽ���Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
11����֪��ԲC��$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��a��b��0��$����M��NΪ����������˵㣬������Բ�ϴ��ڵ�H��ʹ${k_{MH}}{k_{NH}}�ʣ�-\frac{1}{2}��0��$����������e��ȡֵ��ΧΪ��������
| A�� | $��\frac{{\sqrt{2}}}{2}��1��$ | B�� | $��0��\frac{{\sqrt{2}}}{2}��$ | C�� | $��\frac{{\sqrt{3}}}{2}��1��$ | D�� | $��0��\frac{{\sqrt{3}}}{2}��$ |
9����֪����$\overrightarrow{a}$=��5��m����$\overrightarrow{b}$=��2��-2���ң�$\overrightarrow{a}$+$\overrightarrow{b}$����$\overrightarrow{b}$����m=��������
| A�� | -9 | B�� | 9 | C�� | 6 | D�� | -6 |
16����֪��������{an} �У�$\sqrt{{a}_{1}}$+$\sqrt{{a}_{2}}$+��+$\sqrt{{a}_{n}}$=$\frac{n��n+1��}{2}$��n��N*����������{an}��ͨ�ʽΪ��������
| A�� | an=n | B�� | an=n2 | C�� | an=$\frac{n}{2}$ | D�� | an=$\frac{{n}^{2}}{2}$ |
6���ڡ�ABC�У���A��B��C���Եı߷ֱ�Ϊa��b��c����a=1��b=$\sqrt{3}$��A=$\frac{��}{6}$�����B���ڣ�������
| A�� | $\frac{��}{3}$ | B�� | $\frac{��}{6}$ | C�� | $\frac{��}{3}$��$\frac{2��}{3}$ | D�� | $\frac{��}{6}$��$\frac{5��}{6}$ |
13����֪ԲC�ķ���Ϊx2+y2=1��ֱ��l�ķ���Ϊx+y=2����ԲC������һ��P����l�н�Ϊ45���ֱ�߽�l��A����|PA|����СֵΪ��������
| A�� | $\frac{1}{2}$ | B�� | 1 | C�� | $\sqrt{2}-1$ | D�� | $2-\sqrt{2}$ |
10����֪������y2=4x�Ľ���ΪF��ֱ��l��F���������߽���A��B���㣬��|AB|=5����AB�е�ĺ�����Ϊ��������
| A�� | $\frac{5}{2}$ | B�� | 2 | C�� | $\frac{3}{2}$ | D�� | 1 |