题目内容
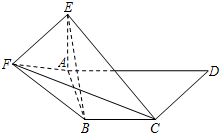 如图,在直角梯形ABCD中,AD∥BC,∠ADC=90°,AE⊥平面ABCD,EF∥CD,BC=CD=AE=EF=
如图,在直角梯形ABCD中,AD∥BC,∠ADC=90°,AE⊥平面ABCD,EF∥CD,BC=CD=AE=EF=| 1 |
| 2 |
(Ⅰ)求证:CE∥平面ABF;
(Ⅱ)求证:BE⊥AF;
(Ⅲ)在直线BC上是否存在点M,使二面角E-MD-A的大小为
| π |
| 6 |
考点:用空间向量求平面间的夹角,与二面角有关的立体几何综合题
专题:空间位置关系与距离,空间向量及应用
分析:(I)作 FG∥EA,AG∥EF,连结EG交AF于H,连结BH,BG,由题设条件推导出四边形AEFG为正方形,从而得到CDAG为平行四边形,由此能够证明CE∥面ABF.
(Ⅱ)利用已知条件推导出BG⊥面AEFG,从而得到AF⊥平面BGE,由此能够证明AF⊥BE.
(Ⅲ)以A为原点,AG为x轴,AE为y轴,AD为z轴,建立空间直角坐标系A-xyz.利用向量法能够求出结果.
(Ⅱ)利用已知条件推导出BG⊥面AEFG,从而得到AF⊥平面BGE,由此能够证明AF⊥BE.
(Ⅲ)以A为原点,AG为x轴,AE为y轴,AD为z轴,建立空间直角坐标系A-xyz.利用向量法能够求出结果.
解答:
 (I)证明:如图,作 FG∥EA,AG∥EF,
(I)证明:如图,作 FG∥EA,AG∥EF,
连结EG交AF于H,连结BH,BG,
∵EF∥CD且EF=CD,
∴AG∥CD,即点G在平面ABCD内.
由AE⊥平面ABCD,知AE⊥AG,
∴四边形AEFG为正方形,
∴CDAG为平行四边形,…(2分)
∴H为EG的中点,B为CG中点,∴BH∥CE,
∴CE∥面ABF.…(4分)
(Ⅱ)证明:∵在平行四边形CDAG中,∠ADC=90°,
∴BG⊥AG.又由AE⊥平面ABCD,知AE⊥BG,
∴BG⊥面AEFG,∴BG⊥AF.…(6分)
又∵AF⊥EG,∴AF⊥平面BGE,
∴AF⊥BE.…(8分)
(Ⅲ)解:如图,以A为原点,AG为x轴,AE为y轴,AD为z轴,
建立空间直角坐标系A-xyz.
由题意得:A(0,0,0),G(1,0,0),E(0,0,1),D(0,2,0),
设M(1,y0,0),则
=(0 , 2 , -1),
=(1,y0-2,0),
设面EMD的一个法向量
=(x,y,z),
则
,令y=1,得z=2,x=2-y0,
∴
=(2-y0,1,2).…(10分)
又∵
⊥面 AMD,
∴
=(0, 0, 1)为面AMD的法向量,
∵二面角E-MD-A的大小为
,
∴|cos<
,
>|=|
|=cos
=
,
解得y0=2±
,
∴在BC上存在点M,且|CM|=|2-(2±
)|=
.…(12分)
 (I)证明:如图,作 FG∥EA,AG∥EF,
(I)证明:如图,作 FG∥EA,AG∥EF,连结EG交AF于H,连结BH,BG,
∵EF∥CD且EF=CD,
∴AG∥CD,即点G在平面ABCD内.
由AE⊥平面ABCD,知AE⊥AG,
∴四边形AEFG为正方形,
∴CDAG为平行四边形,…(2分)
∴H为EG的中点,B为CG中点,∴BH∥CE,
∴CE∥面ABF.…(4分)
(Ⅱ)证明:∵在平行四边形CDAG中,∠ADC=90°,
∴BG⊥AG.又由AE⊥平面ABCD,知AE⊥BG,
∴BG⊥面AEFG,∴BG⊥AF.…(6分)
又∵AF⊥EG,∴AF⊥平面BGE,
∴AF⊥BE.…(8分)
(Ⅲ)解:如图,以A为原点,AG为x轴,AE为y轴,AD为z轴,
建立空间直角坐标系A-xyz.
由题意得:A(0,0,0),G(1,0,0),E(0,0,1),D(0,2,0),
设M(1,y0,0),则
| ED |
| DM |
设面EMD的一个法向量
| n |
则
|
∴
| n |
又∵
| AE |
∴
| AE |
∵二面角E-MD-A的大小为
| π |
| 6 |
∴|cos<
| n |
| AE |
| 2 | ||
1×
|
| π |
| 6 |
| ||
| 2 |
解得y0=2±
| ||
| 3 |
∴在BC上存在点M,且|CM|=|2-(2±
| ||
| 3 |
| ||
| 3 |
点评:本题考查直线与平面垂直的证明,考查直线与直线垂直的证明,考查满足条件的点是否存在的判断,解题时要注意向量法的合理运用.

练习册系列答案
相关题目
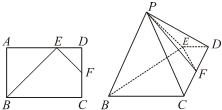 如图,在矩形ABCD中,点E为边AD上的点,点F为边CD的中点,AB=AE=
如图,在矩形ABCD中,点E为边AD上的点,点F为边CD的中点,AB=AE=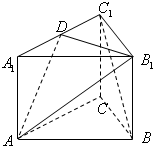 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,底面△ABC是边长为a的正三角形,侧棱长为
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,底面△ABC是边长为a的正三角形,侧棱长为
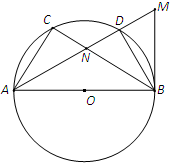 如图,AB是⊙O的一条直径,C,D是⊙O上不同于A,B的两点,过B作⊙O的切线与AD的延长线相交于点M,AD与BC相交于N点,BN=BM.
如图,AB是⊙O的一条直径,C,D是⊙O上不同于A,B的两点,过B作⊙O的切线与AD的延长线相交于点M,AD与BC相交于N点,BN=BM.