题目内容
(1)用辗转相除法求2146与1813的最大公约数.
(2)用秦九韶算法计算函数f(x)=2x5+3x4+2x3-4x+5当x=2时的函数值.
(2)用秦九韶算法计算函数f(x)=2x5+3x4+2x3-4x+5当x=2时的函数值.
考点:用辗转相除计算最大公约数
专题:算法和程序框图
分析:(1)用辗转相除法直接求出两个数的最大公约数.
(2)利用秦九韶算法:f(x)=(((((2x+3)x+2)x+0)x-4)x+5,将x=2代入计算,即可得x=2时的函数值
(2)利用秦九韶算法:f(x)=(((((2x+3)x+2)x+0)x-4)x+5,将x=2代入计算,即可得x=2时的函数值
解答:
解:(1)用辗转相除法求2146与1813的最大公约数.
2146=1813×1+333 1813=333×5+148
333=148×2+37 148=37×4+0
所以2146与1813 的最大公约数是37-------------------------(5分)
(2)根据秦九韶算法,把多项式改写成如下形式:
f(x)=(((((2x+3)x+2)x+0)x-4)x+5
v0=2
v1=v0×2+3=7
v2=v0×2+2=16
v3=v1×2+0=32
v4=v2×2-4=60
v5=v3×2+5=125
所以当x=2时,多项式的值等于125.----------------(10分)
2146=1813×1+333 1813=333×5+148
333=148×2+37 148=37×4+0
所以2146与1813 的最大公约数是37-------------------------(5分)
(2)根据秦九韶算法,把多项式改写成如下形式:
f(x)=(((((2x+3)x+2)x+0)x-4)x+5
v0=2
v1=v0×2+3=7
v2=v0×2+2=16
v3=v1×2+0=32
v4=v2×2-4=60
v5=v3×2+5=125
所以当x=2时,多项式的值等于125.----------------(10分)
点评:本题考查辗转相除法求两个数的最大公约数,用秦九韶算法计算函数的函数值,基本知识的考查.

练习册系列答案
相关题目
已知一个半球的俯视图是一个半径为4的圆,则它的主(正)视图的面积是( )
| A、2π | B、4π | C、8π | D、16π |
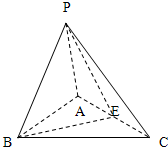 如图,在三棱锥P-ABC中,PA=PB=AB=2,AB⊥BC,平面PAB⊥平面ABC,E为AC的中点.
如图,在三棱锥P-ABC中,PA=PB=AB=2,AB⊥BC,平面PAB⊥平面ABC,E为AC的中点. 如图所示,已知在四面体ABCD中,AB⊥BD,△ABC与△BCD是两个全等的等腰直角三角形,AB=BC=CD.
如图所示,已知在四面体ABCD中,AB⊥BD,△ABC与△BCD是两个全等的等腰直角三角形,AB=BC=CD.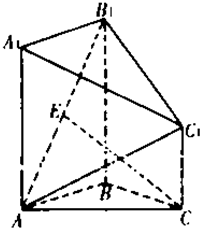 如图,在几何体ABC-A1B1C1中,点A1,B1,C1在平面ABC内的正投影分别为A,B,C,且AB⊥BC,AA1=BB1=4,AB=BC=CC1=2,E为AB1中点,
如图,在几何体ABC-A1B1C1中,点A1,B1,C1在平面ABC内的正投影分别为A,B,C,且AB⊥BC,AA1=BB1=4,AB=BC=CC1=2,E为AB1中点,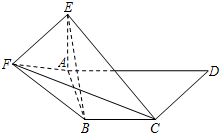 如图,在直角梯形ABCD中,AD∥BC,∠ADC=90°,AE⊥平面ABCD,EF∥CD,BC=CD=AE=EF=
如图,在直角梯形ABCD中,AD∥BC,∠ADC=90°,AE⊥平面ABCD,EF∥CD,BC=CD=AE=EF=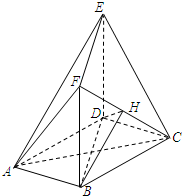 如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.