题目内容
六人按下列要求站一横排,分别有多少种不同的站法?
(1)甲、乙不相邻;
(2)甲、乙之间间隔两人;
(3)甲不站左端,乙不站右端.
(1)甲、乙不相邻;
(2)甲、乙之间间隔两人;
(3)甲不站左端,乙不站右端.
考点:排列、组合的实际应用
专题:应用题,排列组合
分析:(1)先把其余的4个人全排列,然后再把甲乙插入其余4人形成的5个空中,利用乘法原理可得结论;
(2)先将甲、乙以外的4个人作全排列,有
种,然后将甲、乙按条件插入站队,利用乘法原理可得结论;
(3)利用间接法,求出甲在左端的站法有
种,乙在右端的站法有
种,且甲在左端而乙在右端的站法有
种,即可得出结论.
(2)先将甲、乙以外的4个人作全排列,有
| A | 4 4 |
(3)利用间接法,求出甲在左端的站法有
| A | 5 5 |
| A | 5 5 |
| A | 4 4 |
解答:
解:(1)因为甲、乙不相邻,中间有隔档,可用“插空法”,第一步先让甲、乙以外的4个人站队,有
种;第二步再将甲、乙排在4人形成的5个空档(含两端)中,有
种,故共有站法为
=480 (种).
(2)先将甲、乙以外的4个人作全排列,有
种,然后将甲、乙按条件插入站队,有3
种,故共有
•3
=144种站法.
(3)甲在左端的站法有
种,乙在右端的站法有
种,且甲在左端而乙在右端的站法有
种,共有
-2
+
=504种站法.
| A | 4 4 |
| A | 2 5 |
| A | 4 4 |
| A | 2 5 |
(2)先将甲、乙以外的4个人作全排列,有
| A | 4 4 |
| A | 2 2 |
| A | 4 4 |
| A | 2 2 |
(3)甲在左端的站法有
| A | 5 5 |
| A | 5 5 |
| A | 4 4 |
| A | 6 6 |
| A | 5 5 |
| A | 4 4 |
点评:本题主要考查排列组合的实际应用,本题解题的关键是对于有限制的元素要优先排,特殊位置要优先排.相邻的问题用捆绑法,不相邻的问题用插空法,体现了分类讨论的数学思想,是一个中档题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知一个半球的俯视图是一个半径为4的圆,则它的主(正)视图的面积是( )
| A、2π | B、4π | C、8π | D、16π |
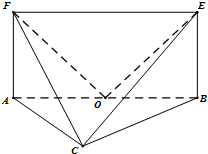 如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,△ABC为等边三角形. O为AB的中点,OF⊥EC.
如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,△ABC为等边三角形. O为AB的中点,OF⊥EC.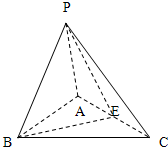 如图,在三棱锥P-ABC中,PA=PB=AB=2,AB⊥BC,平面PAB⊥平面ABC,E为AC的中点.
如图,在三棱锥P-ABC中,PA=PB=AB=2,AB⊥BC,平面PAB⊥平面ABC,E为AC的中点.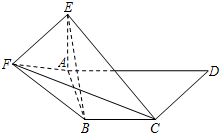 如图,在直角梯形ABCD中,AD∥BC,∠ADC=90°,AE⊥平面ABCD,EF∥CD,BC=CD=AE=EF=
如图,在直角梯形ABCD中,AD∥BC,∠ADC=90°,AE⊥平面ABCD,EF∥CD,BC=CD=AE=EF=