题目内容
是否存在常数a,b,c使得等式1·22+2·32+…+n(n+1)2=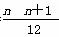 (an2+bn+c)对于一切正整数n都成立?并证明你的结论.
(an2+bn+c)对于一切正整数n都成立?并证明你的结论.
解:假设存在符合题意的常数a,b,c,
在等式1·22+2·32+…+n(n+1)2
=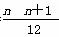 (an2+bn+c)中,
(an2+bn+c)中,
令n=1,得4=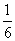 (a+b+c)①
(a+b+c)①
令 n=2,得22=
n=2,得22=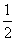 (4a+2b+c)②
(4a+2b+c)②
令n=3,得70=9a+3b+c③
由①②③解得a=3,b=11,c=10,
于是,对于n=1,2,3都有
1·22+2·32+…+n(n+1)2
=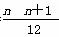 (3n2+11n+10)(*)式成立.
(3n2+11n+10)(*)式成立.
下面用数学归纳法证明:对 于一切正整数n,(*)式都成立.
于一切正整数n,(*)式都成立.
(1)当n=1时,由上述知,(*)式成立.
(2)假设n=k(k∈N*)时,(*)式成立,
即1·22+2·32+…+k(k+1)2
=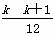 (3k2+11k+10),
(3k2+11k+10),
那么当n=k+1时,
1·22+2·32+…+k(k+1)2+(k+1) (k+2)2
(k+2)2
=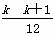 (3k2
(3k2 +11k+10)+(k+1)(k+2)2
+11k+10)+(k+1)(k+2)2
=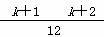 (3k2+5k+12k+24)
(3k2+5k+12k+24)
=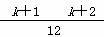 [3(k+1)2+11(k+1)+10],
[3(k+1)2+11(k+1)+10],
由此可知,当n=k+1时,(*)式也成立.
综上所述,当a=3, b=11,c=10时题设的等式对于一切正整数n都成立.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 +3y的最小值为________.
+3y的最小值为________. 76
76 ,则x,y的大小关系是________.
,则x,y的大小关系是________.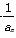 (n=1,2,…).
(n=1,2,…).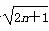 对一切正整数n都成立;
对一切正整数n都成立;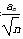 (n=1,2,…),判断bn与bn+1的大小,并说明理由.
(n=1,2,…),判断bn与bn+1的大小,并说明理由.
 ,求这个圆台的侧面积.
,求这个圆台的侧面积.