题目内容
设数列{an} 满足a1=2,an+1=an+
满足a1=2,an+1=an+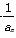 (n=1,2,…).
(n=1,2,…).
(1)证明:an>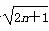 对一切正整数n都成立;
对一切正整数n都成立;
(2)令bn=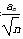 (n=1,2,…),判断bn与bn+1的大小,并说明理由.
(n=1,2,…),判断bn与bn+1的大小,并说明理由.
解:(1)证明:法一:当n=1时,a1=2> ,不等式成立.
,不等式成立.
假设当n=k(k∈N*)时,ak> 成立.
成立.
那么当n=k+1时,a =a
=a +
+ +2>2k+3+
+2>2k+3+ >2(k+1)+1.
>2(k+1)+1.
∴当n=k+1时,ak+1> 成立.
成立.
综上,an> 对一切正整数n都成立.
对一切正整数n都成立.
法二:当n=1时,a1=2> =
= ,结论成立.
,结论成立.
假设当n=k(k∈N*)时结论成立,
即ak> .
.
那么当n=k+1时,由函数f(x)=x+ (x>1)的单调递增性和归纳假设,
(x>1)的单调递增性和归纳假设,
知ak+1=ak+ >
> +
+

 故bn+1<bn.
故bn+1<bn.

练习册系列答案
相关题目
 ,则不等式x2-bx-a<0的解集是( )
,则不等式x2-bx-a<0的解集是( ) D.
D. 
 ,n∈N*,那么f(n+1)-f(n)=( )
,n∈N*,那么f(n+1)-f(n)=( )
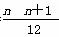 (an2+bn+c)对于一切正整数n都成立?并证明你的结论.
(an2+bn+c)对于一切正整数n都成立?并证明你的结论.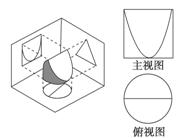
 D.8
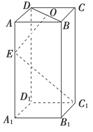
D.8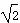 ,OE⊥EC1,求AA1的长
,OE⊥EC1,求AA1的长 .
.