题目内容
5.求椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1的长轴和短轴的长、顶点和焦点的坐标.分析 利用椭圆性质求解.
解答 解:椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1中,
∵a=4,b=2,c=$\sqrt{16-4}$=2$\sqrt{3}$,
∴椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1的长轴2a=8,短轴2b=4,顶点(-4,0),(4,0),(0,-2),(0,2),焦点(-2$\sqrt{3}$,0),(2$\sqrt{3}$,0).
点评 本题考查椭圆的长轴和短轴的长、顶点和焦点的坐标的求法,是基础题,解题时要认真审题,注意椭圆性质的合理运用.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
16.已知圆x2+y2-2x-4y+a=0上有且仅有一个点到直线3x-4y-15=0的距离为1,则实数a的取值情况为( )
| A. | (-∞,5) | B. | -4 | C. | -4或20 | D. | -11 |
13. 设全集U={1,2,3,4,5,6},集合A={1,2,4},B={1,3,5},则下列Venn图中阴影部分表示的集合是( )
设全集U={1,2,3,4,5,6},集合A={1,2,4},B={1,3,5},则下列Venn图中阴影部分表示的集合是( )
 设全集U={1,2,3,4,5,6},集合A={1,2,4},B={1,3,5},则下列Venn图中阴影部分表示的集合是( )
设全集U={1,2,3,4,5,6},集合A={1,2,4},B={1,3,5},则下列Venn图中阴影部分表示的集合是( )| A. | {1} | B. | {2,4} | C. | {3,5} | D. | {2,3,4,5} |
15.2015年山东省东部地区土豆种植形成初步规模,出口商在各地设置了大量的代收点.已知土豆收购按质量标准可分为四个等级,某代收点对等级的统计结果如下表所示:
现从该代售点随机抽取了n袋土豆,其中二级品为恰有40袋.
(Ⅰ)求m、n的值;
(Ⅱ)利用分层抽样的方法从这n袋土豆中抽取10袋,剔除特级品后,再从剩余土豆中任意抽取两袋,求抽取的两袋都是一等品的概率.
| 等级 | 特级 | 一级 | 二级 | 三级 |
| 频率 | 0.30 | 2m | m | 0.10 |
(Ⅰ)求m、n的值;
(Ⅱ)利用分层抽样的方法从这n袋土豆中抽取10袋,剔除特级品后,再从剩余土豆中任意抽取两袋,求抽取的两袋都是一等品的概率.
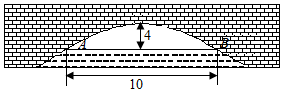 如图,一抛物线型拱桥的拱顶O离水面高4米,水面宽度AB=10米.现有一竹排运送一只货箱欲从桥下经过,已知货箱长20米,宽6米,高2.58米(竹排与水面持平),问货箱能否顺利通过该桥?
如图,一抛物线型拱桥的拱顶O离水面高4米,水面宽度AB=10米.现有一竹排运送一只货箱欲从桥下经过,已知货箱长20米,宽6米,高2.58米(竹排与水面持平),问货箱能否顺利通过该桥?