题目内容
14.已知函数f(x)=|2x-1|+|x+1|.(1)求不等式f(x)≥2的解集;
(2)若关于x的不等式f(x)<a的解集为R,求参数a的取值范围.
分析 (1)通过讨论x的范围,解关于x的不等式,求出x的范围取并集即可;(2)求出f(x)的最小值,从而求出a的范围即可.
解答 解:(1)当$x≥\frac{1}{2}$时,f(x)=3x≥2,得到$x≥\frac{2}{3}$,
当$-1≤x≤\frac{1}{2}$时,f(x)=2-x≥2,得到-1≤x≤0,
当x<-1时,f(x)=-3x≥2,得到x<-1,
综上,不等式解集为$(-∞,0]∪[\frac{2}{3},+∞)$…(5分)
(2)由题意知,f(x)≥a对一切实数x恒成立,
当$x≥\frac{1}{2}$时,$f(x)≥3x≥\frac{3}{2}$,
当$-1≤x≤\frac{1}{2}$时,$f(x)=2-x≥\frac{3}{2}$,
当x<-1时,f(x)=-3x>3.
综上,$f{(x)_{min}}=\frac{3}{2}$.故$a≤\frac{3}{2}$…(10分)
点评 本题考查了解绝对值不等式问题,考查分类讨论思想,是一道中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.已知实数a、b满足a2+b2=1,设函数f(x)=x2-4x+5,则使f(a)≥f(b)的概率为( )
| A. | $\frac{3}{4}+\frac{1}{2π}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}+\frac{1}{π}$ |
19.(文科)学业水平考试后,某校对高二学生的数学、英语成绩进行了统计,结果如下(人数):
已知英语、数学的优秀率分别为24%、30%(注:合格人数中不包含优秀人数).
(1)求a、b的值;
(11)现按照英语成绩的等级,采用分层抽样的方法,从数学不合格的学生中选取6人,若再从这6人中任选2人,求这两名学生的英语成绩恰为一人优秀一人合格的概率.
| 项目 | 数学 | |||
| 优秀 | 合格 | 不合格 | ||
| 英 语 | 优秀 | 70 | 30 | 20 |
| 合格 | 60 | 240 | b | |
| 不合格 | a | 20 | 10 | |
(1)求a、b的值;
(11)现按照英语成绩的等级,采用分层抽样的方法,从数学不合格的学生中选取6人,若再从这6人中任选2人,求这两名学生的英语成绩恰为一人优秀一人合格的概率.

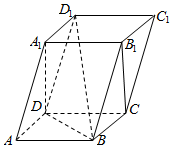 在四棱柱ABCD-A1B1C1D1中,底面ABCD是正方形,侧面BCC1B1⊥底面ABCD,B1C=CD=2,BB1=2$\sqrt{2}$.
在四棱柱ABCD-A1B1C1D1中,底面ABCD是正方形,侧面BCC1B1⊥底面ABCD,B1C=CD=2,BB1=2$\sqrt{2}$.