题目内容
16．已知圆x2+y2-2x-4y+a=0上有且仅有一个点到直线3x-4y-15=0的距离为1，则实数a的取值情况为（ ）| A． | （-∞，5） | B． | -4 | C． | -4或20 | D． | -11 |
分析 由已知得圆心（1，2）到直线3x-4y-15=0的距离d=r+1，由此能求出实数a的取值．
解答 解：∵圆x2+y2-2x-4y+a=0上有且仅有一个点到直线3x-4y-15=0的距离为1，
∴圆心（1，2）半径r=$\frac{1}{2}\sqrt{20-4a}$，
∴圆心（1，2）到直线3x-4y-15=0的距离d=r+1，
∴d=$\frac{|3-8-15|}{\sqrt{9+16}}$=$\frac{1}{2}\sqrt{20-4a}$+1，
解得a=-4．
故选：B．
点评 本题考查实数值的求法，是基础题，解题时要认真审题，注意点到直线的距离公式的合理运用．
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
6．P为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上异于左右顶点A1，A2的任意一点，则直线PA1与PA2的斜率之积为定值-$\frac{{b}^{2}}{{a}^{2}}$，将这个结论类比到双曲线，得出的结论为：P为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）上异于左右顶点A1，A2的任意一点，则（ ）
| A． | 直线PA1与PA2的斜率之和为定值$\frac{{a}^{2}}{{b}^{2}}$ | |
| B． | 直线PA1与PA2的斜率之积为定值$\frac{{a}^{2}}{{b}^{2}}$ | |
| C． | 直线PA1与PA2的斜率之和为定值$\frac{{b}^{2}}{{a}^{2}}$ | |
| D． | 直线PA1与PA2的斜率之积为定值$\frac{{b}^{2}}{{a}^{2}}$ |
如图，F是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右焦点，O是坐标原点，|OF|=$\sqrt{5}$，过F作OF的垂线交椭圆于P0，Q0两点，△OP0Q0的面积为$\frac{4\sqrt{5}}{3}$．
11．已知集合A={0，l，3}，B={x|x2-3x=0}，则A∩B=（ ）
| A． | {0} | B． | {0，1} | C． | {0，3} | D． | {0，1，3} |
1．直线3x-4y-4=0被圆x2+y2-6x=0截得的弦长为（ ）
| A． | $2\sqrt{2}$ | B． | 4 | C． | $4\sqrt{2}$ | D． | 2 |
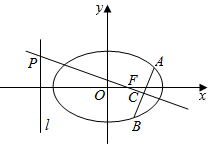如图，在平面直角坐标系xOy中，己知椭圆$\frac{x^2}{2}+{y^2}$=1的右焦点F，直线x=-2，过F的直线与椭圆交于A、B两点（AB与x轴不垂直），线段的垂直平分线分别交直线L和AB于点P、C．若PC=2AB，求直线AB的方程．