题目内容
20.△ABC内角A、B、C所对的边分别为a、b、c,已知向量$\overrightarrow m=(a+c,b-a)$,$\overrightarrow n=(a-c,b)$,且$\overrightarrow m⊥\overrightarrow n$,则sinA+sinB的最大值是$\sqrt{3}$.分析 由向量垂直列方程得出a,b,c的关系,利用余弦定理解出C,用A表示出B,使用三角函数的恒等变换化简sinA+sinB得出最大值.
解答 解:∵$\overrightarrow{m}⊥\overrightarrow{n}$,∴(a+c)(a-c)+b(b-a)=0,即a2+b2-c2=ab.
∴cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}=\frac{1}{2}$.
∴C=$\frac{π}{3}$.
∴B=$\frac{2π}{3}-A$.
∴sinA+sinB=sinA+sin($\frac{2π}{3}-A$)=$\frac{3}{2}sinA$+$\frac{\sqrt{3}}{2}cosA$=$\sqrt{3}$sin(A+$\frac{π}{6}$).
∵0$<A<\frac{2π}{3}$,∴$\frac{π}{6}<$A+$\frac{π}{6}$<$\frac{5π}{6}$.
∴当A+$\frac{π}{6}$=$\frac{π}{2}$时,sinA+sinB取得最大值$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查了平面向量的垂直与数量积的关系,余弦定理,三角函数的恒等变换,属于中档题.

练习册系列答案
相关题目
11.已知集合A={0,l,3},B={x|x2-3x=0},则A∩B=( )
| A. | {0} | B. | {0,1} | C. | {0,3} | D. | {0,1,3} |
15.某班有男、女优秀少先队员各2名,现需选出2名优秀少先队员到社区做公益宣传活动,则选出的两名队员性别相同的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
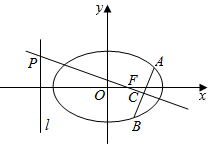 如图,在平面直角坐标系xOy中,己知椭圆$\frac{x^2}{2}+{y^2}$=1的右焦点F,直线x=-2,过F的直线与椭圆交于A、B两点(AB与x轴不垂直),线段的垂直平分线分别交直线L和AB于点P、C.若PC=2AB,求直线AB的方程.
如图,在平面直角坐标系xOy中,己知椭圆$\frac{x^2}{2}+{y^2}$=1的右焦点F,直线x=-2,过F的直线与椭圆交于A、B两点(AB与x轴不垂直),线段的垂直平分线分别交直线L和AB于点P、C.若PC=2AB,求直线AB的方程.