题目内容
17.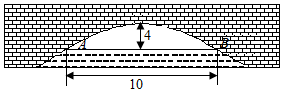 如图,一抛物线型拱桥的拱顶O离水面高4米,水面宽度AB=10米.现有一竹排运送一只货箱欲从桥下经过,已知货箱长20米,宽6米,高2.58米(竹排与水面持平),问货箱能否顺利通过该桥?
如图,一抛物线型拱桥的拱顶O离水面高4米,水面宽度AB=10米.现有一竹排运送一只货箱欲从桥下经过,已知货箱长20米,宽6米,高2.58米(竹排与水面持平),问货箱能否顺利通过该桥?
分析 可以O为坐标原点,AB的垂线为y轴建立平面直角坐标系,从而根据条件即可求出抛物线的方程为${x}^{2}=-\frac{25}{4}y$,根据条件可以设C(3,-4),过C作AB的垂线交抛物线于D(3,y0),带入抛物线方程便可求出y0,从而可求出|CD|的值,与货箱的高2.58比较便可判断出货箱能否顺利通过该桥.
解答 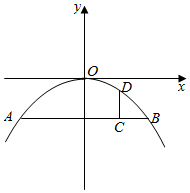 解:以O为原点,过O垂直于AB的直线为y轴,建立如图所示平面直角坐标系:
解:以O为原点,过O垂直于AB的直线为y轴,建立如图所示平面直角坐标系:
设抛物线方程为x2=my,根据题意知点B(5,-4)在抛物线上;
∴25=-4m;
∴$m=-\frac{25}{4}$;
∴${x}^{2}=-\frac{25}{4}y$;
可设C(3,-4),过C作AB的垂线,交抛物线于D(3,y0),则$9=-\frac{25}{4}{y}_{0}$;
∴${y}_{0}=-\frac{36}{25}$;
∴$|CD|=\frac{36}{25}<2.58$;
∴货箱不能顺利通过该桥.
点评 考查通过建立平面直角坐标系,利用曲线方程解决实际问题的方法,抛物线的标准方程,待定系数法求抛物线的方程,以及抛物线上点的坐标和抛物线方程的关系.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
2.已知实数a、b满足a2+b2=1,设函数f(x)=x2-4x+5,则使f(a)≥f(b)的概率为( )
| A. | $\frac{3}{4}+\frac{1}{2π}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}+\frac{1}{π}$ |
7.若x,y满足不等式组$\left\{\begin{array}{l}{2x-3y-6≥0}\\{x+y-3≥0}\\{x≤a}\end{array}\right.$,z=x-y的最大值为4,则实数a=( )
| A. | 4 | B. | $\frac{7}{2}$ | C. | 5 | D. | $\frac{9}{2}$ |
 如图,F是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,O是坐标原点,|OF|=$\sqrt{5}$,过F作OF的垂线交椭圆于P0,Q0两点,△OP0Q0的面积为$\frac{4\sqrt{5}}{3}$.
如图,F是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,O是坐标原点,|OF|=$\sqrt{5}$,过F作OF的垂线交椭圆于P0,Q0两点,△OP0Q0的面积为$\frac{4\sqrt{5}}{3}$.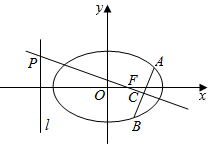 如图,在平面直角坐标系xOy中,己知椭圆$\frac{x^2}{2}+{y^2}$=1的右焦点F,直线x=-2,过F的直线与椭圆交于A、B两点(AB与x轴不垂直),线段的垂直平分线分别交直线L和AB于点P、C.若PC=2AB,求直线AB的方程.
如图,在平面直角坐标系xOy中,己知椭圆$\frac{x^2}{2}+{y^2}$=1的右焦点F,直线x=-2,过F的直线与椭圆交于A、B两点(AB与x轴不垂直),线段的垂直平分线分别交直线L和AB于点P、C.若PC=2AB,求直线AB的方程.