题目内容
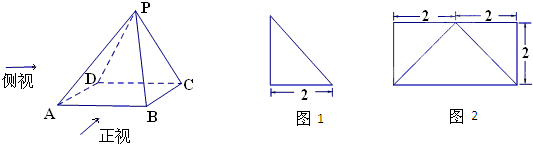
已知四棱锥P-ABCD的正视图是一个底边长为4、腰长为3的等腰三角形，图1、图2分别是四棱锥P-ABCD的侧视图和俯视图．求四棱锥P-ABCD的侧面PAB和PBC的面积．
考点：棱柱、棱锥、棱台的侧面积和表面积
专题：空间位置关系与距离
分析：取CD的中点E，连接PE、AE．由三视图的形状并结合面面垂直、线面垂直的性质，算出PE，PF，利用三角形全等，判断三角形的形状，可算出△PAB的面积，然后求解三角形PAC的面积．
解答：
解：依题意，可知点P在平面ABCD上的正射影是线段CD的中点E，连接PE，
则PE⊥平面ABCD．…（2分）
在等腰三角形PCD中，PC=PD=3，DE=EC=2，
在Rt△PED中，PE=
=
，…（4分）
过E作E⊥AB，垂足为F，则F为AB中点，连接PF，…（5分）
在Rt△PEF中，PF=
=3，…（6分）
∵Rt△ADE≌Rt△BEC，∴AE=BE
∴Rt△PAE≌Rt△PBE，∴PA=PB，
∵F为中点
∴AB⊥PF．…（8分）
∴△PAB的面积为S=
AB•PF=6．…（9分）
∵PE⊥平面ABCD，BC?平面ABCD，
∴BC⊥PE．
∵BC⊥CD，CD∩PE=C，
∴BC⊥平面PCD．…（11分）
∵PC?平面PCD，∴BC⊥PC
依题意得PC=3，BC=2．
∴△PBC的面积为S=
BC•PC=3．…（13分）
则PE⊥平面ABCD．…（2分）
在等腰三角形PCD中，PC=PD=3，DE=EC=2，
在Rt△PED中，PE=
| PD2+DE2 |
| 5 |
过E作E⊥AB，垂足为F，则F为AB中点，连接PF，…（5分）
在Rt△PEF中，PF=
| PE2+EF2 |
∵Rt△ADE≌Rt△BEC，∴AE=BE
∴Rt△PAE≌Rt△PBE，∴PA=PB，
∵F为中点
∴AB⊥PF．…（8分）
∴△PAB的面积为S=
| 1 |
| 2 |
∵PE⊥平面ABCD，BC?平面ABCD，
∴BC⊥PE．
∵BC⊥CD，CD∩PE=C，
∴BC⊥平面PCD．…（11分）
∵PC?平面PCD，∴BC⊥PC
依题意得PC=3，BC=2．
∴△PBC的面积为S=
| 1 |
| 2 |
点评：本题给出三视图，要求我们证明线线垂直并求侧面三角形的面积，着重考查了三视图求面积和面面垂直、线面垂直的性质定理等知识，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
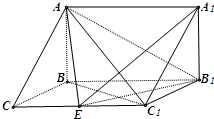如图，在三棱柱ABC-A1B1C1中，已知BC=1，BB1=2，∠BCC1=90°，AB⊥侧面BB1C1C．
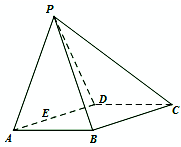如图所示，在四棱锥P-ABCD中，四边形ABCD为菱形，△PAD为等边三角形，平面PAD⊥平面ABCD，且∠DAB=60°，AB=2，E为AD的中点．
如图，在四棱锥P-ABCD中，底面ABCD为菱形，∠BAD=60°，Q为AD的中点．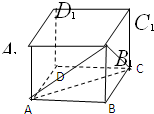
已知正方体ABCD-A1B1C1D1的棱长是a，求三棱锥B-AB1C的高．