题目内容
已知数列{an}的前n项和Sn=10n-n2(n∈N*),求:
(1)求数列{an}的通项公式;
(2)求{|an|}的前n项和Tn.
(1)求数列{an}的通项公式;
(2)求{|an|}的前n项和Tn.
考点:数列的求和,数列递推式
专题:综合题,等差数列与等比数列
分析:(1)利用递推公式当n≥2,an=Sn-Sn-1,a1=S1可求;
(2)根据an,求出bn表达式,然后根据式子的特点求数列{bn}的前n项和Tn.
(2)根据an,求出bn表达式,然后根据式子的特点求数列{bn}的前n项和Tn.
解答:
解:(1)由Sn=10n-n2,
可得Sn-1=10(n-1)-(n-1)2,(n≥2)
两式相减可得an=-2n+11,
∵n=1时,a1=S1=10-1=9,满足上式,
∴an=-2n+11;
(2)n≤5时,bn=an=-2n+11,Tn=10n-n2.
n≥6时,bn=an=2n-11,
Tn=(a1+a2+…+a5)-(a6+a7+…+an)=2S5-Sn=50-10n+n2
故Tn=
.
可得Sn-1=10(n-1)-(n-1)2,(n≥2)
两式相减可得an=-2n+11,
∵n=1时,a1=S1=10-1=9,满足上式,
∴an=-2n+11;
(2)n≤5时,bn=an=-2n+11,Tn=10n-n2.
n≥6时,bn=an=2n-11,
Tn=(a1+a2+…+a5)-(a6+a7+…+an)=2S5-Sn=50-10n+n2
故Tn=
|
点评:本题主要考查数列求和的计算,根据条件求出an和的bn表达式是解决本题的关键,注意要对n进行讨论.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
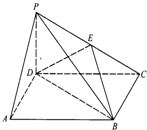 如图,四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是正方形,PD=AB=2,E为PC中点.
如图,四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是正方形,PD=AB=2,E为PC中点.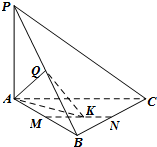 如图,在三棱锥P-ABC中,直线PA⊥平面ABC,且∠ABC=90°,又点Q,M,N分别是线段PB,AB,BC的中点,且点K是线段MN上的动点.
如图,在三棱锥P-ABC中,直线PA⊥平面ABC,且∠ABC=90°,又点Q,M,N分别是线段PB,AB,BC的中点,且点K是线段MN上的动点.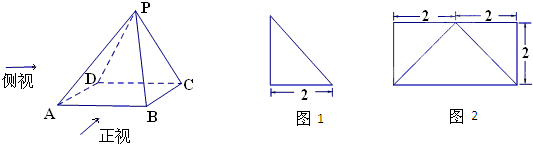
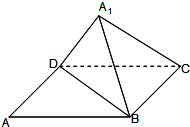 如图,已知矩形ABCD中,AB=10,BC=6,将矩形沿对角线BD把△ABD折起,使A移到A1点,且A1在平面BCD上的射影O恰好在CD上.
如图,已知矩形ABCD中,AB=10,BC=6,将矩形沿对角线BD把△ABD折起,使A移到A1点,且A1在平面BCD上的射影O恰好在CD上.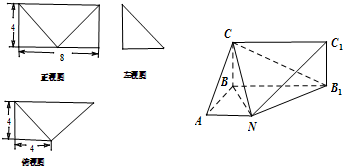 已知某几何体的直观图和三视图如下图所示,其正视图为矩形,左视图为等腰直角三角形,俯视图为直角梯形.
已知某几何体的直观图和三视图如下图所示,其正视图为矩形,左视图为等腰直角三角形,俯视图为直角梯形.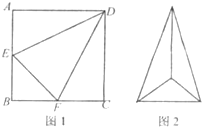 如图1,边长为2的d正方形ABCD中,E,F 分别是AB,BC的中点,将△ADE,△CDF,△BEF折起,使A,C,B二点重合于G,所得二棱锥G-DEF的俯视图如图2,则其正视图的面积为
如图1,边长为2的d正方形ABCD中,E,F 分别是AB,BC的中点,将△ADE,△CDF,△BEF折起,使A,C,B二点重合于G,所得二棱锥G-DEF的俯视图如图2,则其正视图的面积为