题目内容
设光线从点A(-2,2)出发,经过x轴反射后经过点B(0,1),则光线与x轴的交点坐标为 .
考点:与直线关于点、直线对称的直线方程
专题:直线与圆
分析:设光线与x轴的交点坐标为C(a,0),则由题意可得,直线AC和直线BC关于直线x=a对称,它们的倾斜角互补,斜率互为相反数,即 KAC=-KBC,求得a的值,可得答案.
解答:
解:设光线与x轴的交点坐标为C(a,0),则由题意可得,
直线AC和直线BC关于直线x=a对称,它们的倾斜角互补,斜率互为相反数,
即 KAC=-KBC,即
= -
,解得 a=-
,
故答案为:(-
,0).
直线AC和直线BC关于直线x=a对称,它们的倾斜角互补,斜率互为相反数,
即 KAC=-KBC,即
| 2-0 |
| -2-a |
| 1-0 |
| 0-a |
| 2 |
| 3 |
故答案为:(-
| 2 |
| 3 |
点评:本题主要考查反射定律、对称问题的,判断直线AC和直线BC关于直线x=a对称,它们的倾斜角互补,斜率互为相反数,是解题的关键,属于中档题.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目

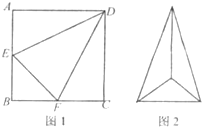 如图1,边长为2的d正方形ABCD中,E,F 分别是AB,BC的中点,将△ADE,△CDF,△BEF折起,使A,C,B二点重合于G,所得二棱锥G-DEF的俯视图如图2,则其正视图的面积为
如图1,边长为2的d正方形ABCD中,E,F 分别是AB,BC的中点,将△ADE,△CDF,△BEF折起,使A,C,B二点重合于G,所得二棱锥G-DEF的俯视图如图2,则其正视图的面积为