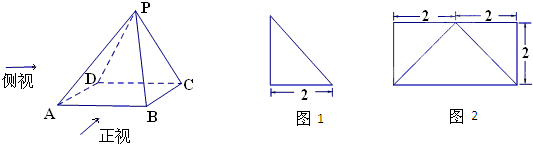
题目内容
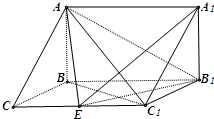 如图,在三棱柱ABC-A1B1C1中,已知BC=1,BB1=2,∠BCC1=90°,AB⊥侧面BB1C1C.
如图,在三棱柱ABC-A1B1C1中,已知BC=1,BB1=2,∠BCC1=90°,AB⊥侧面BB1C1C.(1)求直线C1B与底面ABC所成角的正弦值;
(2)若E为CC1的中点,AB=
| 2 |
考点:与二面角有关的立体几何综合题
专题:空间位置关系与距离
分析:(1)由已知条件推导出CC1⊥平面ABC,∠C1BC中为直线C1B与底面ABC所成角,由此能求出直线C1B与底面ABC所成角的正弦值.
(2)由题设条件推导出异面直线A1B1与AE的夹角∠EAB等于二面角A-EB1-A1的平面角的大小,由此能求出平面AEB1与平面A1EB1的夹角.
(2)由题设条件推导出异面直线A1B1与AE的夹角∠EAB等于二面角A-EB1-A1的平面角的大小,由此能求出平面AEB1与平面A1EB1的夹角.
解答:
解:(1)∵BC=1,BB1=2,∠BCC1=90°,AB丄侧面BB1C1C,
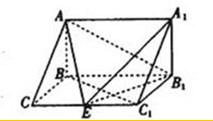 ∴CC1⊥平面ABC,
∴CC1⊥平面ABC,
在Rt△BCC1中,∠C1BC中为直线C1B与底面ABC所成角
∵BC=1,BB1=2,∠BCC1=90°,
∴BC1=
=
,
∴sin∠C1BC=
=
=
.
∴直线C1B与底面ABC所成角的正弦值为
.
(2)∵A1B1∥AB,∴A1B1⊥侧面BB1C1C,
∴A1B1⊥EB1,且EB1在面A1EB1内,
∵EA⊥EB1,EA在面AEB1内,
即A1B1,AE分别在两个半平面内,均和棱EB1垂直,
∴异面直线A1B1与AE的夹角∠EAB等于二面角A-EB1-A1的平面角的大小,
∵AB=
,EB=1,
∴tan∠EAB=
=
,
∴平面AEB1与平面A1EB1的夹角为arctan
.
 ∴CC1⊥平面ABC,
∴CC1⊥平面ABC,在Rt△BCC1中,∠C1BC中为直线C1B与底面ABC所成角
∵BC=1,BB1=2,∠BCC1=90°,
∴BC1=
| 4+1 |
| 5 |
∴sin∠C1BC=
| CC1 |
| BC1 |
| 2 | ||
|
2
| ||
| 5 |
∴直线C1B与底面ABC所成角的正弦值为
2
| ||
| 5 |
(2)∵A1B1∥AB,∴A1B1⊥侧面BB1C1C,
∴A1B1⊥EB1,且EB1在面A1EB1内,
∵EA⊥EB1,EA在面AEB1内,
即A1B1,AE分别在两个半平面内,均和棱EB1垂直,
∴异面直线A1B1与AE的夹角∠EAB等于二面角A-EB1-A1的平面角的大小,
∵AB=
| 2 |
∴tan∠EAB=
| BE |
| AB |
| ||
| 2 |
∴平面AEB1与平面A1EB1的夹角为arctan
| ||
| 2 |
点评:本题考查直线与平面所成角的大小的求法,考查二面角的求法,解题时要注意空间思维能力的培养.

练习册系列答案
相关题目
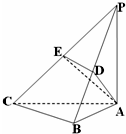 已知三棱锥P-ABC,∠PAC=∠ABC=90°,PA=AC=2BC,平面PAC⊥平面ABC,D、E分别是PB、PC的中点.
已知三棱锥P-ABC,∠PAC=∠ABC=90°,PA=AC=2BC,平面PAC⊥平面ABC,D、E分别是PB、PC的中点. 已知平行四边形ABCD和矩形ACEF所在的平面互相垂直,AB=1,AD=2,∠ADC=60°,AF=a(a>0)
已知平行四边形ABCD和矩形ACEF所在的平面互相垂直,AB=1,AD=2,∠ADC=60°,AF=a(a>0)