题目内容
目标函数z=2x+y,变量x,y满足
,则有( )
|
| A、zmin=4,无最大值 | ||
B、zmax=
| ||
| C、z既无最大值,也无最小值 | ||
D、zmin=0,zmax=
|
考点:简单线性规划
专题:不等式的解法及应用
分析:先根据题意画出线性可行域,然后做出直线2x+y=0,再利用平移的方法求出最值.
解答:
 解:根据变量x,y满足
解:根据变量x,y满足
,画出可行域如下:
作出直线L:2x+y=0,据图可知,将直线L平移至A点时,可行域内的点使目标函数z取最小值,无最大值.
由
得A(1,2),
∴zmin=4,无最大值.
故选:A.
 解:根据变量x,y满足
解:根据变量x,y满足
|
作出直线L:2x+y=0,据图可知,将直线L平移至A点时,可行域内的点使目标函数z取最小值,无最大值.
由
|
∴zmin=4,无最大值.
故选:A.
点评:这是一道线性规划问题,主要是考查可行域的画法,以及在理解目标函数z的几何意义的基础上,采用合理方式求最值的方法.

练习册系列答案
相关题目
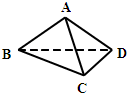 如图,四面体A-BCD中,AB=AD=CD=1,BD=
如图,四面体A-BCD中,AB=AD=CD=1,BD=| 2 |
A、
| ||||
| B、3π | ||||
C、
| ||||
| D、2π |
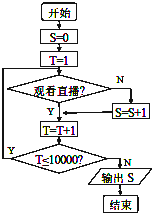 为了解“伦敦奥运会开幕式”电视直播节目的收视情况,某机构在某地随机抽查了10000人,把抽查结果输入如图所示的程序框图中,其输出的数值是3700,则该节目的收视率为( )
为了解“伦敦奥运会开幕式”电视直播节目的收视情况,某机构在某地随机抽查了10000人,把抽查结果输入如图所示的程序框图中,其输出的数值是3700,则该节目的收视率为( )| A、3700 | B、630 |
| C、0.63 | D、0.37 |
用5,6,7,8,9组成没有重复数字的五位数,其中个位和万位都是偶数的五位数的个数是( )
| A、36 | B、48 | C、72 | D、12 |
X大学2014年自主招生报名刚结束,某考生想知道这次报考的人数,他随机记录了50个考生的考号;已知考生的考号是从0001,0002,0003,…这样从小到大依次顺序排列.经计算,这50个考号的和是24966(其中0001+0002视为3),据此,估计2014年参加X大学自主招生的考生数约为( )
| A、500人 | B、1000人 |
| C、1500人 | D、2000人 |
函数f(x)=x-1的零点是( )
| A、0 | B、1 |
| C、(0,0) | D、(1,0) |