题目内容
16.袋中装有除颜色外形状大小完全相同的6个小球,其中有4个编号为1,2,3,4的红球,2个编号为A、B的黑球,现从中任取2个小球.(Ⅰ)求所取取2个小球都是红球的概率;
(Ⅱ)求所取的2个小球颜色不相同的概率.
分析 (Ⅰ)利用列举法求出任取2个小球的基本事件总数,用M表示“所取取2个小球都是红球”,利用列举法求出M包含的基本事件个数,由此能求出所取取2个小球都是红球的概率.
(Ⅱ)用N表示“所取的2个小球颜色不相同”,利用列举法求出N包含的基本事件个数,由此能求出所取的2个小球颜色不相同的概率.
解答 解:(Ⅰ)由题意知,任取2个小球的基本事件有:
{1,2},{1,3},{1,4},{1,A},{1,B},{2,3},{2,4},{2,A},
{2,B},{3,4},{3,A},{3,B},{4,A},{4,B},{A,B},共15个,
用M表示“所取取2个小球都是红球”,
则M包含的基本事件有:
{1,2},{1,4},{2,3},{2,4},{3,4},共6个,
∴所取取2个小球都是红球的概率:P(M)=$\frac{6}{15}$=$\frac{2}{5}$.
(Ⅱ)用N表示“所取的2个小球颜色不相同”,
则N包含的基本事件有:
{1,A},{1,B},{2,A},{2,B},{3,A},{3,B},{4,A},{4,B},共8个,
∴所取的2个小球颜色不相同的概率:P(N)=$\frac{8}{15}$.
点评 本题考查古典概型等基础知识,考查推理论证能力、运算求解能力、数据处理能力,考查化归与转化思想,是基础题.

练习册系列答案
相关题目
6.已知抛物线C:y2=4x,过焦点F且斜率为$\sqrt{3}$的直线与C相交于P,Q两点,且P,Q两点在准线上的投影分别为M,N两点,则S△MFN=( )
| A. | $\frac{8}{3}$ | B. | $\frac{{8\sqrt{3}}}{3}$ | C. | $\frac{16}{3}$ | D. | $\frac{{16\sqrt{3}}}{3}$ |
7.如图是秦九韶算法的一个程序框图,则输出的S为( )
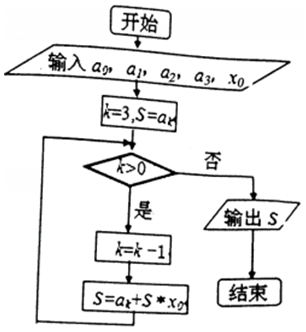

| A. | a1+x0(a3+x0(a0+a2x0))的值 | B. | a3+x0(a2+x0(a1+a0x0))的值 | ||
| C. | a0+x0(a1+x0(a2+a3x0))的值 | D. | a2+x0(a0+x0(a3+a1x0))的值 |
4.已知P={x|x2+2x-3<0},Q={-2,-1,0,1,2},则P∩Q=( )
| A. | {-1,0,1} | B. | {-2,-1,0,1} | C. | {-2,-1,0} | D. | {-1,0} |
1.已知约束条件为$\left\{\begin{array}{l}2x-y-6≤0\\ x-y+2≥0\end{array}\right.$,若目标函数z=kx+y仅在交点(8,10)处取得最小值,则k的取值范围为( )
| A. | (-2,-1) | B. | (-∞,-2)∪(-1,+∞) | C. | (-∞,-2) | D. | (-1,+∞) |
8.在数列{an}中,a1=1,a2=2,且${a_{n+2}}-{a_n}=1+{(-1)^n}$(n∈N+),则S100=( )
| A. | 0 | B. | 1300 | C. | 2600 | D. | 2602 |
6.设a,b≠0,则“a>b”是“$\frac{1}{a}<\frac{1}{b}$”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
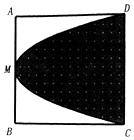 如图,在边长为2的正方形ABCD中,M是AB的中点,则过C,M,D三点的抛物线与CD围成阴影部分,在正方形ABCD中任取一点P,则点P恰好取自阴影部分的概率为$\frac{2}{3}$.
如图,在边长为2的正方形ABCD中,M是AB的中点,则过C,M,D三点的抛物线与CD围成阴影部分,在正方形ABCD中任取一点P,则点P恰好取自阴影部分的概率为$\frac{2}{3}$.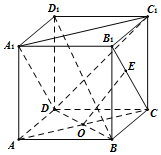 在棱长为1的正方体ABCD-A1B1C1D1中,AC∩BD=O,E是线段B1C(含端点)上的一动点,则
在棱长为1的正方体ABCD-A1B1C1D1中,AC∩BD=O,E是线段B1C(含端点)上的一动点,则