题目内容
1．已知约束条件为$\left\{\begin{array}{l}2x-y-6≤0\\ x-y+2≥0\end{array}\right.$，若目标函数z=kx+y仅在交点（8，10）处取得最小值，则k的取值范围为（ ）| A． | （-2，-1） | B． | （-∞，-2）∪（-1，+∞） | C． | （-∞，-2） | D． | （-1，+∞） |
分析 由约束条件作出可行域，化目标函数为直线方程的斜截式，结合目标函数z=kx+y仅在交点（8，10）处取得最小值即可求得k的取值范围．
解答 解：由约束条件$\left\{\begin{array}{l}2x-y-6≤0\\ x-y+2≥0\end{array}\right.$作出可行域如图，
联立$\left\{\begin{array}{l}{2x-y-6=0}\\{x-y+2=0}\end{array}\right.$，解得A（8，10），
化目标函数z=kx+y为y=-kx+z，
∵目标函数z=kx+y仅在交点（8，10）处取得最小值，
∴-k＞2，则k＜-2．
∴k的取值范围为（-∞，-2）．
故选：C．
点评 本题考查简单的线性规划，考查了数形结合的解题思想方法，是中档题．
练习册系列答案
精英口算卡系列答案
相关题目
6．已知复数z满足：$\frac{{z（1+i）{i^3}}}{1-i}=1-i$，则复数z的虚部为（ ）
| A． | i | B． | -i | C． | 1 | D． | -1 |
13．
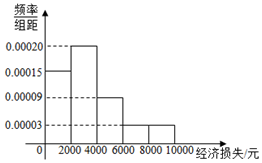2016年10月21日，台风“海马”导致江苏、福建、广东3省11市51个县（市、区）189.9万人受灾，某调查小组调查了受灾某小区的100户居民由于台风造成的经济损失，将收集的数据分成[0，2000]，（2000，4000]，（4000，6000]，（6000，8000]，（8000，10000]五组，并作出频率分布直方图．
（Ⅰ）台风后居委会号召小区居民为台风重灾区捐款，小张调查的100户居民捐款情况如表所示，在表格空白处填写正确数字，并说明能否在犯错误的概率不超过0.05的前提下认为捐款数额超过或不超过500元和自身经济损失是否超过4000元有关？
（Ⅱ）将上述调查所得到的频率视为概率，现在从该地区大量受灾居民中，采用随机抽样的方法每次抽取1户居民，抽取3次，记被抽取的3户居民中自身经济损失超过4000元的人数为ξ，若每次抽取的结果是相互独立的，求ξ的分布列，期望E（ξ）和方差D（ξ）．
附：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d
2016年10月21日，台风“海马”导致江苏、福建、广东3省11市51个县（市、区）189.9万人受灾，某调查小组调查了受灾某小区的100户居民由于台风造成的经济损失，将收集的数据分成[0，2000]，（2000，4000]，（4000，6000]，（6000，8000]，（8000，10000]五组，并作出频率分布直方图．（Ⅰ）台风后居委会号召小区居民为台风重灾区捐款，小张调查的100户居民捐款情况如表所示，在表格空白处填写正确数字，并说明能否在犯错误的概率不超过0.05的前提下认为捐款数额超过或不超过500元和自身经济损失是否超过4000元有关？
（Ⅱ）将上述调查所得到的频率视为概率，现在从该地区大量受灾居民中，采用随机抽样的方法每次抽取1户居民，抽取3次，记被抽取的3户居民中自身经济损失超过4000元的人数为ξ，若每次抽取的结果是相互独立的，求ξ的分布列，期望E（ξ）和方差D（ξ）．
| 经济损失不超过4000元 | 经济损失超过4000元 | 总计 | |
| 捐款超过500元 | 60 | ||
| 捐款不超过500元 | 10 | ||
| 总计 |
| P（K2≥k0） | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
11．若集合A={x|x-x2＞0}，B={x|（x+1）（m-x）＞0}，则“m＞1”是“A∩B≠∅”的（ ）
| A． | 充分而不必要条件 | B． | 必要而不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |