题目内容
12.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点(0,1),且离心率e=$\frac{\sqrt{3}}{2}$.(Ⅰ)求椭圆C的方程;
(Ⅱ)已知直线l与椭圆C交于A(x1,y1),B(x2,y2)两点,且△OAB的面积为S,其中O为坐标原点,当S取得最大值时,求y${\;}_{1}^{2}$+y${\;}_{2}^{2}$的值.
分析 (Ⅰ)运用离心率公式,结合a,b,c的关系,解方程可得a,进而得到椭圆方程;
(Ⅱ)设直线l的方程为x=my+t,代入椭圆方程可得(4+m2)y2+2mty+t2-4=0,运用韦达定理和弦长公式,以及点到直线的距离公式,三角形的面积公式,结合基本不等式即可得到最大值,计算化简即可得到所求值为1.
解答 解:(Ⅰ)由题意可得b=1,且e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,
a2-b2=c2,
解得a=2,c=$\sqrt{3}$,
即有椭圆的方程为$\frac{{x}^{2}}{4}$+y2=1;
(Ⅱ)设直线l的方程为x=my+t,
代入椭圆方程可得(4+m2)y2+2mty+t2-4=0,
判别式为4m2t2-4(4+m2)(t2-4)>0,
即为4+m2>t2,
y1+y2═-$\frac{2mt}{4+{m}^{2}}$,y1y2=$\frac{{t}^{2}-4}{4+{m}^{2}}$,
则S=$\frac{1}{2}$d•|AB|=$\frac{1}{2}$$\frac{|t|}{\sqrt{1+{m}^{2}}}$•$\sqrt{1+{m}^{2}}$•$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$
=$\frac{1}{2}$|t|•$\sqrt{\frac{4{m}^{2}{t}^{2}}{(4+{m}^{2})^{2}}-\frac{4{t}^{2}-16}{4+{m}^{2}}}$
=$\frac{\sqrt{{t}^{2}(4+{m}^{2}-{t}^{2})}}{4+{m}^{2}}$≤$\frac{\frac{{t}^{2}+4+{m}^{2}-{t}^{2}}{2}}{4+{m}^{2}}$=$\frac{1}{2}$,
当且仅当t2=4+m2-t2,即4+m2=2t2,S取得最大值$\frac{1}{2}$.
即有y${\;}_{1}^{2}$+y${\;}_{2}^{2}$=(y1+y2)2-2y1y2=(-$\frac{2mt}{4+{m}^{2}}$)2-2•$\frac{{t}^{2}-4}{4+{m}^{2}}$
=$\frac{{m}^{2}}{{t}^{2}}$-$\frac{{t}^{2}-4}{{t}^{2}}$=$\frac{4+{m}^{2}-{t}^{2}}{{t}^{2}}$=$\frac{2{t}^{2}-{t}^{2}}{{t}^{2}}$=1.
点评 本题考查椭圆的方程的求法,注意运用离心率公式,考查三角形的面积的最值的求法,注意运用点到直线的距离公式和弦长公式,以及基本不等式的运用,考查化简整理的运算能力,属于中档题.

 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案| A. | (2,1) | B. | (-2,-1) | C. | (2,1)或(-2,-1) | D. | (2,-1)或(-2,1) |
| A. | ?x0∈A,x0∈B | B. | ?x0∈A,x0∈B | C. | A∩B=A | D. | A∩(∁uB)≠∅ |
①经过直线外一点有且只有一条直线与已知直线平行
②经过直线外一点有且只有一条直线与已知直线垂直
③经过平面外一点有且只有一个平面与已知平面平行
④经过平面外一点有且只有一个平面与已知平面垂直.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 执行如图的程序框图,若输入k=63,则输出的n=( )
执行如图的程序框图,若输入k=63,则输出的n=( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
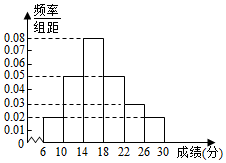 某省去年高三200000名考生英语听力考试服从正态分布N(17,9),现从某校高三年级随机抽取50名考生的成绩,发现全部介于[6,30]之间,将成绩按如图方式分成6组:第1组[6,10),第2组[10,14),…,第6组[26,30),如图是按上述分组方法得到的频率分布直方图.
某省去年高三200000名考生英语听力考试服从正态分布N(17,9),现从某校高三年级随机抽取50名考生的成绩,发现全部介于[6,30]之间,将成绩按如图方式分成6组:第1组[6,10),第2组[10,14),…,第6组[26,30),如图是按上述分组方法得到的频率分布直方图.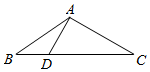 如图,已知点D在△ABC的BC边上,且∠DAC=90°,cosC=$\frac{\sqrt{6}}{3}$,AB=6,BD=$\sqrt{6}$,则ADsin∠BAD=.
如图,已知点D在△ABC的BC边上,且∠DAC=90°,cosC=$\frac{\sqrt{6}}{3}$,AB=6,BD=$\sqrt{6}$,则ADsin∠BAD=.