题目内容
13.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$均为单位向量,它们的夹角为$\frac{2π}{3}$,则|$\overrightarrow{a}$+$\overrightarrow{b}$|=( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
分析 由条件即可得到$|\overrightarrow{a}|=1,|\overrightarrow{b}|=1$,且$\overrightarrow{a},\overrightarrow{b}$夹角为$\frac{2π}{3}$,从而进行数量积的运算便可求出$|\overrightarrow{a}+\overrightarrow{b}{|}^{2}=1$,从而便可得出$|\overrightarrow{a}+\overrightarrow{b}|$的值.
解答 解:根据题意,$|\overrightarrow{a}|=|\overrightarrow{b}|=1$,$<\overrightarrow{a},\overrightarrow{b}>=\frac{2π}{3}$;
∴$|\overrightarrow{a}+\overrightarrow{b}{|}^{2}={\overrightarrow{a}}^{2}+2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}$=$1+2•1•1•cos\frac{2π}{3}+1=1$;
∴$|\overrightarrow{a}+\overrightarrow{b}|=1$.
故选:A.
点评 考查单位向量的概念,向量夹角的概念,以及向量数量积的运算及计算公式.

练习册系列答案
相关题目
3.已知集合A、B是非空集合且A⊆B,则下列说法错误的是( )
| A. | ?x0∈A,x0∈B | B. | ?x0∈A,x0∈B | C. | A∩B=A | D. | A∩(∁uB)≠∅ |
1. 执行如图的程序框图,若输入k=63,则输出的n=( )
执行如图的程序框图,若输入k=63,则输出的n=( )
 执行如图的程序框图,若输入k=63,则输出的n=( )
执行如图的程序框图,若输入k=63,则输出的n=( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
8.向量$\overrightarrow a=(3,-4),|\overrightarrow b|=2$,若$\overrightarrow a•\overrightarrow b=-5$,则向量$\overrightarrow a,\overrightarrow b$的夹角为( )
| A. | 60° | B. | 30° | C. | 135° | D. | 120° |
18.复数z满足(z-1)(1+i)=2i,则|z|=( )
| A. | 1 | B. | 2 | C. | $\sqrt{5}$ | D. | 5 |
5.已知复数$z=\frac{i}{i+1}$,那么复数z对应的点位于复平面内的( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
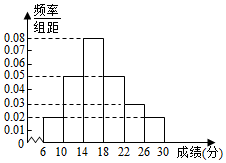 某省去年高三200000名考生英语听力考试服从正态分布N(17,9),现从某校高三年级随机抽取50名考生的成绩,发现全部介于[6,30]之间,将成绩按如图方式分成6组:第1组[6,10),第2组[10,14),…,第6组[26,30),如图是按上述分组方法得到的频率分布直方图.
某省去年高三200000名考生英语听力考试服从正态分布N(17,9),现从某校高三年级随机抽取50名考生的成绩,发现全部介于[6,30]之间,将成绩按如图方式分成6组:第1组[6,10),第2组[10,14),…,第6组[26,30),如图是按上述分组方法得到的频率分布直方图.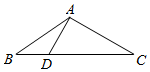 如图,已知点D在△ABC的BC边上,且∠DAC=90°,cosC=$\frac{\sqrt{6}}{3}$,AB=6,BD=$\sqrt{6}$,则ADsin∠BAD=.
如图,已知点D在△ABC的BC边上,且∠DAC=90°,cosC=$\frac{\sqrt{6}}{3}$,AB=6,BD=$\sqrt{6}$,则ADsin∠BAD=.