��Ŀ����
3������˵����ȷ���ǣ�������| A�� | ��?a��R������ax2-2x+a=0����ʵ�����ķ�Ϊ��?a��R������ax2-2x+a=0�и�ʵ���� | |
| B�� | ���⡰a��b��R����a2+b2=0����a=b=0������������ǡ�a��b��R����a��0����b��0����a2+b2��0�� | |
| C�� | ����p�����ع鷽��Ϊ$\stackrel{��}{y}$-x=1����y��x����أ�����q������1��2��3��4����λ����2��3��������p��qΪ������ | |
| D�� | ��X��N��1��4������P��X��t2-1��=P��X��2t��������һ����ֲ���Ҫ����t=1 |
���� ��4������ֱ�����жϣ����ɵó����ۣ�
��� �⣺��?a��R������ax2-2x+a=0����ʵ�����ķ�Ϊ��?a��R������ax2-2x+a=0û����ʵ��������A����ȷ��
���⡰a��b��R����a2+b2=0����a=b=0������������ǡ�a��b��R����a��0��b��0����a2+b2��0������B����ȷ��
����p�����ع鷽��Ϊ$\stackrel{��}{y}$-x=1����y��x����أ��Ǽ����⣻����q������1��2��3��4����λ����2.5���Ǽ����⣬������p��qΪ�����⣬��C����ȷ��
��X��N��1��4������P��X��t2-1��=P��X��2t�������ɵ�t2-1+2t=2����t=1��3����P��X��t2-1��=P��X��2t��������һ����ֲ���Ҫ����t=1����D��ȷ��
��ѡD
���� ���⿼������ķ�������⡢�������������жϣ�������̬�ֲ�������ѧ��������������������֪ʶ�ۺ���ǿ��

��ϰ��ϵ�д�
 ���ٴ�����ɽ����ϵ�д�
���ٴ�����ɽ����ϵ�д�
�����Ŀ
18����x��$\sqrt{x}$-$\frac{1}{x}$��9��չ��ʽ�У�x��ϵ��Ϊ��������
| A�� | 36 | B�� | -36 | C�� | 84 | D�� | -84 |
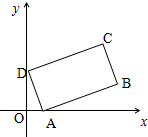 ��ͼ������ABCD��AD�ߵij�Ϊ1��AB�ߵij�Ϊ2������ABCDλ�ڵ�һ���ޣ��Ҷ���A��D�ֱ�λ��x�ᡢy����������ϣ���ԭ�㣩��������$\overrightarrow{OB}•\overrightarrow{OC}$�����ֵ��6��
��ͼ������ABCD��AD�ߵij�Ϊ1��AB�ߵij�Ϊ2������ABCDλ�ڵ�һ���ޣ��Ҷ���A��D�ֱ�λ��x�ᡢy����������ϣ���ԭ�㣩��������$\overrightarrow{OB}•\overrightarrow{OC}$�����ֵ��6�� ��ͼ����ƽ���ı���ABCD�У���֪$\overrightarrow{|AB|}$=8��$\overrightarrow{|AD|}$=5��$\overrightarrow{CP}=3\overrightarrow{PD}$��$\overrightarrow{AP}•\overrightarrow{BP}=2$����$\overrightarrow{AB}•\overrightarrow{AD}$=22��
��ͼ����ƽ���ı���ABCD�У���֪$\overrightarrow{|AB|}$=8��$\overrightarrow{|AD|}$=5��$\overrightarrow{CP}=3\overrightarrow{PD}$��$\overrightarrow{AP}•\overrightarrow{BP}=2$����$\overrightarrow{AB}•\overrightarrow{AD}$=22��