题目内容
3.已知a、b是两条不同直线,α、β、γ是三个不同平面,给出以下命题:①若α∥β,β∥γ,则α∥γ;
②若α⊥β,β⊥γ,则α∥γ;
③若a⊥α,a⊥β,则α∥β;
④若a⊥α,b⊥β,α⊥β,则a⊥b.
以上命题中真命题的个数是3.
分析 ①根据面面平行的性质定理进行判断.
②根据面面垂直的性质进行判断.
③根据线面垂直的性质进行判断.
④根据线面垂直和面面垂直的性质进行判断.
解答 解:①若α∥β,β∥γ,则α∥γ正确,同时和一个平面都平行的两个平面是平行的;故①正确,
②若α⊥β,β⊥γ,则α∥γ错误,同时和一个平面都垂直的两个平面可能是平行的也可能是相交的;故②错误
③若a⊥α,a⊥β,则α∥β正确,同时和一条直线垂直的两个平面是平行的;故③正确;
④若a⊥α,α⊥β,则a∥β或a?平面β,b⊥β,则a⊥b成立,故④正确,
故正确的是①③④.
故答案为:3
点评 本题主要考查命题的真假判断,涉及空间直线和平面,平面和平面平行或垂直的判断,根据相应的判定定理和性质定理是解决本题的关键.

练习册系列答案
相关题目
3.下列说法正确的是( )
| A. | “?a∈R,方程ax2-2x+a=0有正实根”的否定为“?a∈R,方程ax2-2x+a=0有负实数” | |
| B. | 命题“a、b∈R,若a2+b2=0,则a=b=0”的逆否命题是“a、b∈R,若a≠0,且b≠0,则a2+b2≠0” | |
| C. | 命题p:若回归方程为$\stackrel{∧}{y}$-x=1,则y与x负相关;命题q:数据1,2,3,4的中位数是2或3,则命题p∨q为真命题 | |
| D. | 若X~N(1,4),则P(X<t2-1)=P(X>2t)成立的一个充分不必要条件t=1 |
14.在圆O的直径CB的延长线上取一点A,AP与圆O切于点P,且∠APB=30°,AP=$\sqrt{3}$,则CP=( )
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2$\sqrt{3}$-1 | D. | 2$\sqrt{3}$+1 |
11.执行如图所示的程序框图,若输入的x,y∈R,则输出t的最大值为( )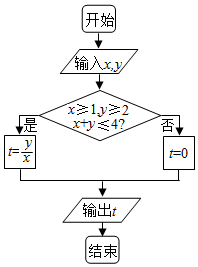

| A. | 1 | B. | 3 | C. | 2 | D. | 0 |
18.在(x-$\frac{a}{x}$)5的展开式中x3的系数等于5,则该展开式中二项式系数最大的项的系数为( )
| A. | 20 | B. | -10 | C. | -10,10 | D. | 10 |
15.i为虚数单位,复数$\frac{2+i}{1-i}$=( )
| A. | $\frac{1}{2}$+$\frac{3}{2}$i | B. | $\frac{3}{2}$+$\frac{1}{2}i$ | C. | $\frac{3}{2}$+$\frac{3}{2}$i | D. | $\frac{3}{2}$-$\frac{1}{2}$i |
12.若复数z=$\frac{3+2i}{1-i}$(i为虚数单位),则z的共轭复数$\overline{z}$为( )
| A. | $\frac{1}{2}$+$\frac{5}{2}$i | B. | $\frac{1}{2}$-$\frac{5}{2}$i | C. | $\frac{1}{2}$+2i | D. | $\frac{1}{2}$-2i |
 某公司要在一条笔直的道路边安装路灯,要求灯柱AB与地面垂直,灯杆BC与灯柱AB所在的平面与道路走向垂,路灯C采用锥形灯罩,射出的光线与平面ABC的部分截面如图中阴影部分所示.已知∠ABC=$\frac{2}{3}$π,∠ACD=$\frac{π}{3}$,路宽AD=24米.设∠BAC=θ$(\frac{π}{12}≤θ≤\frac{π}{6})$
某公司要在一条笔直的道路边安装路灯,要求灯柱AB与地面垂直,灯杆BC与灯柱AB所在的平面与道路走向垂,路灯C采用锥形灯罩,射出的光线与平面ABC的部分截面如图中阴影部分所示.已知∠ABC=$\frac{2}{3}$π,∠ACD=$\frac{π}{3}$,路宽AD=24米.设∠BAC=θ$(\frac{π}{12}≤θ≤\frac{π}{6})$ 某赛季甲、乙两名篮球运动员每场比赛得分的原始记录如下:
某赛季甲、乙两名篮球运动员每场比赛得分的原始记录如下: