题目内容
17．不等式组$\left\{\begin{array}{l}y≥0\\ x+3y≤4\\ 3x+y≥4\end{array}\right.$，所表示的平面区域的面积等于（ ）| A． | $\frac{3}{2}$ | B． | $\frac{2}{3}$ | C． | $\frac{4}{3}$ | D． | $\frac{3}{4}$ |
分析 由约束条件作出可行域，把可行域的面积化为两个三角形的面积求解．
解答 解：由约束条件$\left\{\begin{array}{l}y≥0\\ x+3y≤4\\ 3x+y≥4\end{array}\right.$作出可行域如图，
∴S四边形OBAC=S△OBA+S△OCA
=$\frac{1}{2}×\frac{4}{3}×1+\frac{1}{2}×\frac{4}{3}×1=\frac{4}{3}$．
故选：C．
点评 本题考查简单的线性规划，考查了数形结合的解题思想方法，是中档题．
练习册系列答案
应用题作业本系列答案
相关题目
8．已知角α的终边经过点$P（-1，\sqrt{3}）$，则cosα=（ ）
| A． | $\frac{{\sqrt{3}}}{2}$ | B． | $-\frac{{\sqrt{3}}}{2}$ | C． | $\frac{1}{2}$ | D． | $-\frac{1}{2}$ |
5．已知i是虚数单位，m，n∈R，则“m=n=1”是“m2-1-2ni=-2i”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
2．函数y=$\frac{ln（x+1）}{{\sqrt{{3^x}-27}}}$的定义域为（ ）
| A． | （-1，+∞） | B． | （-1，3） | C． | （3，+∞） | D． | [3，+∞） |
9．
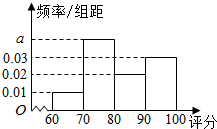为检测某种零件的生产质量，检验人员需抽取同批次的零件样本进行检测指标评分．若检测后评分结果大于60分的零件为合格零件，评分结果不超过40分的零件将直接被淘汰，评分结果在（40，60]内的零件可能被修复也可能被淘汰．现检验员小张检测出200个合格零件，根据指标评分绘制的频率分布直方图如图所示．
（1）求出频率分布与直方图中a的值；
（2）估计这200个零件评分结果的平均数和中位数；
（2）根据已有的经验，可能被修复的零件个体被修复的概率如表：
假设每个零件被修复与否相互独立．现有5个零件的检测指标评分结果为（单位：分）：38，43，45，52，58，
①求这5个零件中，至多有2个不被修复而淘汰的概率；
②记这5个零件被修复的个数为随机变量X，求X的分布列和数学期望．
为检测某种零件的生产质量，检验人员需抽取同批次的零件样本进行检测指标评分．若检测后评分结果大于60分的零件为合格零件，评分结果不超过40分的零件将直接被淘汰，评分结果在（40，60]内的零件可能被修复也可能被淘汰．现检验员小张检测出200个合格零件，根据指标评分绘制的频率分布直方图如图所示．（1）求出频率分布与直方图中a的值；
（2）估计这200个零件评分结果的平均数和中位数；
（2）根据已有的经验，可能被修复的零件个体被修复的概率如表：
| 零件评分结果所在区间 | （40，50] | （50，60] |
| 每个零件个数被修复的概率 | $\frac{1}{3}$ | $\frac{1}{2}$ |
①求这5个零件中，至多有2个不被修复而淘汰的概率；
②记这5个零件被修复的个数为随机变量X，求X的分布列和数学期望．