题目内容
6.化简下列各式:(1)$\frac{{a}^{2}\root{3}{{a}^{2}b}}{\sqrt{ab}}$;
(2)$\frac{(b\sqrt{ab})^{3}\root{3}{{a}^{2}b}}{\root{3}{a{b}^{2}}}$.
分析 分别化根式为分数指数幂化简两式得答案.
解答 解:(1)$\frac{{a}^{2}\root{3}{{a}^{2}b}}{\sqrt{ab}}$=$\frac{{a}^{2}•{a}^{\frac{2}{3}}•{b}^{\frac{1}{3}}}{{a}^{\frac{1}{2}}•{b}^{\frac{1}{2}}}$=${a}^{2+\frac{2}{3}-\frac{1}{2}}•{b}^{\frac{1}{3}-\frac{1}{2}}$=$\frac{\root{6}{{a}^{13}}}{\root{6}{b}}$;
(2)$\frac{(b\sqrt{ab})^{3}\root{3}{{a}^{2}b}}{\root{3}{a{b}^{2}}}$=$\frac{b•{a}^{\frac{3}{2}}•{b}^{\frac{3}{2}}•{a}^{\frac{2}{3}}•{b}^{\frac{1}{3}}}{{a}^{\frac{1}{3}}•{b}^{\frac{2}{3}}}$=${a}^{\frac{3}{2}+\frac{2}{3}-\frac{1}{3}}•{b}^{1+\frac{3}{2}+\frac{1}{3}-\frac{2}{3}}$=$\root{6}{{a}^{11}}•\root{6}{{b}^{13}}$.
点评 本题考查有理指数幂的化简与求值,考查了根式与分数指数幂的互化,是基础的计算题.

练习册系列答案
相关题目
17.不等式组$\left\{\begin{array}{l}y≥0\\ x+3y≤4\\ 3x+y≥4\end{array}\right.$,所表示的平面区域的面积等于( )
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
18.己知α是第三象限角,且tanα=$\frac{5}{12}$,则cosα的值是( )
| A. | -$\frac{5}{13}$ | B. | $\frac{5}{13}$ | C. | $\frac{12}{13}$ | D. | -$\frac{12}{13}$ |
 如图所示,正方体ABCD-A′B′C′D′的棱长为1,E、F分别是棱AA′,CC′的中点,过直线E,F的平面分别与棱BB′、DD′交于M、N,设BM=x,x∈(0,1),给出以下四个命题:
如图所示,正方体ABCD-A′B′C′D′的棱长为1,E、F分别是棱AA′,CC′的中点,过直线E,F的平面分别与棱BB′、DD′交于M、N,设BM=x,x∈(0,1),给出以下四个命题: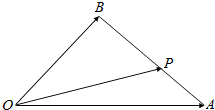 如图,在△AOB中,已知P为线段AB上的一点,且$\overrightarrow{BP}$=2$\overrightarrow{PA}$.
如图,在△AOB中,已知P为线段AB上的一点,且$\overrightarrow{BP}$=2$\overrightarrow{PA}$.