题目内容
已知F1，F2分别是双曲线C：
-
=1的左、右两个焦点．若C上存在一点P，使得|
|•|
|=2a2，则C的离心率e的取值范围是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| PF1 |
| PF2 |
A、（1，
| ||
B、[
| ||
C、（1，
| ||
D、[
|
考点：双曲线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：根据双曲线的性质，得到双曲线上点到焦点的距离大于等于a+c，或c-a，建立不等式关系即可得到结论．
解答：
解：∵|
|•|
|≥（a+c）（c-a）=c2-a2，
∴若C上存在一点P，使得|
|•|
|=2a2，
则2a2≥c2-a2，
即c2≤3a2，即e2≤3，
则e≤
，
∵e＞1，
∴1＜e≤
，
故选：C
| PF1 |
| PF2 |
∴若C上存在一点P，使得|
| PF1 |
| PF2 |
则2a2≥c2-a2，
即c2≤3a2，即e2≤3，
则e≤
| 3 |
∵e＞1，
∴1＜e≤
| 3 |
故选：C
点评：本题主要考查双曲线离心率的求解，根据双曲线上的点，到焦点的距离的取值范围是解决本题的关键．
练习册系列答案
相关题目
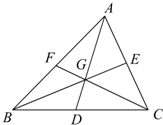在△ABC中，AD，BE，CF分别是BC，CA，AB边上的中线，G是它们的交点，则下列等式中不正确的是（ ）A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
设A（-2，
），椭圆3x2+4y2=48的右焦点是F，点P在椭圆上移动，当|AP|+2|PF|取最小值时P点的坐标是（ ）
| 3 |
A、（0，2
| ||||
B、（0，-2
| ||||
C、（2
| ||||
D、（-2
|
双曲线两条渐近线的夹角为60°，该双曲线的离心率为（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
下列命题正确的是（ ）
| A、a∥b，a⊥α⇒a⊥b |
| B、a⊥α，b⊥α⇒a∥b |
| C、a⊥α，a⊥b⇒b∥α |
| D、a∥α，a⊥b⇒b⊥α |
函数f（x）=lgx+x-3的零点所在的区间是（ ）
| A、（1，2） |
| B、（3，4） |
| C、（2，3） |
| D、（0，1） |
如图，四棱锥P-ABCD中，底面ABCD是矩形，PA=AB=1，AD=