题目内容
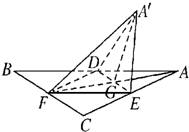如图，等边三角形ABC的中线AF与中位线DE相交于G，已知△A′ED是△ADE绕DE旋转过程中的一个图形，下列命题中，错误的是（ ）| A、动点A′在平面ABC上的射影在线段AF上 |
| B、恒有平面A′GF⊥平面ACDE |
| C、三棱锥′-EFD的体积有最大值 |
| D、异面直线A′E与BD不可能垂直 |
考点：异面直线及其所成的角
专题：空间位置关系与距离
分析：由斜线的射影定理可判断A正确；由面面垂直的判定定理，可判断B正确；由三棱锥的体积公式，可判断C正确；由异面直线所成的角的概念可判断D不正确．
解答：
解：∵A′D=A′E，△ABC是正三角形，
∴A′在平面ABC上的射影在线段AF上，故A正确；
由A知，平面A′GF一定过平面BCED的垂线，
∴恒有平面A′GF⊥平面BCED，故B正确；
三棱锥A′-FED的底面积是定值，体积由高即A′到底面的距离决定，
当平面A′DE⊥平面BCED时，三棱锥A′-FED的体积有最大值，故C正确；
当（A′E）2+EF2=（A′F）2时，面直线A′E与BD垂直，故④错误．
故选：D．
∴A′在平面ABC上的射影在线段AF上，故A正确；
由A知，平面A′GF一定过平面BCED的垂线，
∴恒有平面A′GF⊥平面BCED，故B正确；
三棱锥A′-FED的底面积是定值，体积由高即A′到底面的距离决定，
当平面A′DE⊥平面BCED时，三棱锥A′-FED的体积有最大值，故C正确；
当（A′E）2+EF2=（A′F）2时，面直线A′E与BD垂直，故④错误．
故选：D．
点评：本题考查了线面、面面垂直的判定定理、性质定理的运用，考查了空间线线、线面的位置关系及所成的角的概念，考查了空间想象能力．
练习册系列答案
相关题目
下列函数中，最小正周期是
的偶函数为（ ）
| π |
| 2 |
| A、y=tan2x | ||
B、y=cos（4x+
| ||
| C、y=2cos22x-1 | ||
| D、y=cos2x |
双曲线两条渐近线的夹角为60°，该双曲线的离心率为（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
归纳推理是（ ）
| A、特殊到一般的推理 |
| B、特殊到特殊的推理 |
| C、一般到特殊的推理 |
| D、一般到一般的推理 |
函数f（x）=lgx+x-3的零点所在的区间是（ ）
| A、（1，2） |
| B、（3，4） |
| C、（2，3） |
| D、（0，1） |
在平面直角坐标系xOy中，抛物线y2=2px上一点到焦点F的距离与到y轴的距离的差为1．