题目内容
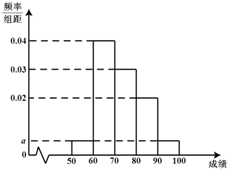 某校为了了解学生数学学习情况,随机抽取60位学生期中考试数学成绩,并作出频率分布直方图如图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100),
某校为了了解学生数学学习情况,随机抽取60位学生期中考试数学成绩,并作出频率分布直方图如图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100),(Ⅰ)求图中a的值,并根据频率分布直方图估计该校学生数学成绩的平均分;
(Ⅱ)若这60名学生的数学成绩某些分数段的人数(x)与语文成绩相应分数段的人数(y)之比如下表所示,求语文成绩在[50,90)之外的人数.
| 分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
| x:y | 1:1 | 2:1 | 3:4 | 4:5 |
考点:频率分布表,频率分布直方图
专题:概率与统计
分析:(Ⅰ)根据频率和为1,求出a的值,再计算平均数;
(II)先求出60位学生数学成绩各分数段内的人数,按照表中所给比例,再求出语文成绩在各分数段的人数即可.
(II)先求出60位学生数学成绩各分数段内的人数,按照表中所给比例,再求出语文成绩在各分数段的人数即可.
解答:
解:(Ⅰ)根据频率和为1,得
(2a+0.02+0.03+0.04)×10=1,
解得a=0.005;
∴估计平均数为
0.05×55+0.4×65+0.3×75+0.2×85+0.05×95=73;…(6分)
(II)这60位学生数学成绩在[90,100]的分别有3人、24人、18人、12人,
按照表中所给比例,语文成绩在[50,60)、[60,70)、[70,80)、[80,90)的
分别有3人、12人、24人、15人,共54人,
∴语文成绩在[50,90)之外的人数有60-54=6人.…(12分)
(2a+0.02+0.03+0.04)×10=1,
解得a=0.005;
∴估计平均数为
0.05×55+0.4×65+0.3×75+0.2×85+0.05×95=73;…(6分)
(II)这60位学生数学成绩在[90,100]的分别有3人、24人、18人、12人,
按照表中所给比例,语文成绩在[50,60)、[60,70)、[70,80)、[80,90)的
分别有3人、12人、24人、15人,共54人,
∴语文成绩在[50,90)之外的人数有60-54=6人.…(12分)
点评:本题考查了频率分布表的应用问题,解题时应熟悉频率和等于1,利用频率表计算平均数等知识,是基础题.

练习册系列答案
相关题目
某单位有职工75人,其中青年职工35人,中年职工25人,老年职工15人,为了了解该单位职工的健康情况,用分层抽样的方法从中抽取样本,若样本中的青年职工人数为7,则样本容量为( )
| A、7 | B、15 | C、25 | D、35 |
设复数z满足(1+i)
=2-i(i为虚数单位,
表示复数z的共轭复数),则在复平面上复数z对应的点( )
 |
| z |
 |
| z |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |