题目内容
已知函数f(x)=sin(2x+
)+sin(2x-
)+cos2x-sin2x+a的在区间[0,
]上的最小值为0.
(Ⅰ)求常数a的值;
(Ⅱ)当x∈[0,π]时,求使f(x)≥0成立的x的集合.
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
(Ⅰ)求常数a的值;
(Ⅱ)当x∈[0,π]时,求使f(x)≥0成立的x的集合.
考点:两角和与差的正弦函数,正弦函数的单调性
专题:三角函数的图像与性质
分析:利用两角和与差的三角函数式化简f(x)为一个角的一个三角函数的形式,然后解答.
解答:
解:(Ⅰ)因为f(x)=sin(2x+
)+sin(2x-
)+cos2x-sin2x+a
=
sin2x+
cos2x+
sin2x-
cos2x+cos2x+a,
所以f(x)=
sin2x+cos2x+a,
所以f(x)=2sin(2x+
)+a.
因为x∈[0,
]时,2x+
∈[
,
],
所以x=
时,f(x)的取得最小值f(
)=-1+a.
依题意,-1+a=0,所以a=1.
(Ⅱ)由(Ⅰ)知f(x)=2sin(2x+
)+1.
要使f(x)≥0,即sin(2x+
)≥-
.
所以2kπ-
≤2x+
≤2kπ+
,k∈Z,即kπ-
≤x≤kπ+
,k∈Z.
当k=0时,-
≤x≤
;当k=1时,
≤x≤
.
又x∈[0,π],故使f(x)≥0成立的x的集合是[0,
]∪[
,π].
| π |
| 6 |
| π |
| 6 |
=
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
所以f(x)=
| 3 |
所以f(x)=2sin(2x+
| π |
| 6 |
因为x∈[0,
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
所以x=
| π |
| 2 |
| π |
| 2 |
依题意,-1+a=0,所以a=1.
(Ⅱ)由(Ⅰ)知f(x)=2sin(2x+
| π |
| 6 |
要使f(x)≥0,即sin(2x+
| π |
| 6 |
| 1 |
| 2 |
所以2kπ-
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
| π |
| 6 |
| π |
| 2 |
当k=0时,-
| π |
| 6 |
| π |
| 2 |
| 5π |
| 6 |
| 3π |
| 2 |
又x∈[0,π],故使f(x)≥0成立的x的集合是[0,
| π |
| 2 |
| 5π |
| 6 |
点评:本题考查了两角和与差的三角函数公式的运用化简三角函数解析式为最简形式,然后解答相关问题;关键是正确化简.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
空间直角坐标系中A(1,2,3),B(-1,0,5),C(3,0,4),D(4,1,3),则直线AB与CD的位置关系是( )
| A、平行 | B、垂直 |
| C、相交但不垂直 | D、无法确定 |
执行如图的程序框图,若p=5,则输出的S值为( )


A、
| ||
B、
| ||
C、
| ||
D、
|
函数y=x3-3x+k有三个不同的零点,则k的取值范围是( )
| A、(2,+∞) |
| B、(-2,2) |
| C、(-∞,-,2) |
| D、[-2,2] |
设a=log
4,b=3
,c=(
)0.4,则有( )
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| A、a<b<c |
| B、a<c<b |
| C、c<a<b |
| D、c<b<a |
幂函数f(x)的图象过点(4,
),那么f(
)的值为( )
| 1 |
| 2 |
| 1 |
| 16 |
A、
| ||
| B、2 | ||
| C、1 | ||
| D、4 |
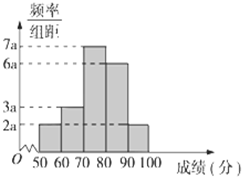 某校为了了解学生的数学学习情况,以5%的比例随机抽取20位学生,根据他们的期中考试数学成绩作出频率分布直方图如右图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100),
某校为了了解学生的数学学习情况,以5%的比例随机抽取20位学生,根据他们的期中考试数学成绩作出频率分布直方图如右图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100),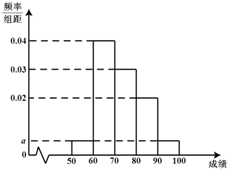 某校为了了解学生数学学习情况,随机抽取60位学生期中考试数学成绩,并作出频率分布直方图如图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100),
某校为了了解学生数学学习情况,随机抽取60位学生期中考试数学成绩,并作出频率分布直方图如图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100),