题目内容

求证：函数f（x）=
x
x2-1
在（1，+∞）上是减函数．
考点：函数单调性的判断与证明
专题：导数的概念及应用
分析：直接求解函数的导数，然后，判断其导数的取值情况即可．
解答： 证明：
∵f（x）=
x
x2-1
，
∴f′（x）=
x2-1-2x2
(x2-1)2

=-
1+2x2
(x2-1)2
＜0，
∴f（x）在（1，+∞）上为减函数．
点评：本题重点考查了函数的单调性与导数的关系、求导公式等知识属于中档题．
练习册系列答案
相关题目
一个几何体的三视图如图所示，则该几何体的体积是
 
．
已知椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为e，直线y=ex+a与x，y轴分别交于A，B两点，E点是直线与椭圆的一个交点，且AE=e•AB，则离心率e的值为
 
．
计算：
（1）（2
7
9
） 
1
2
+（lg5）0+（
27
64
） -
1
3
；              
（2）log3
427
3
+lg25+lg4+7log72．
函数y=tan
π
4
-sin
5π
4
sin（
7π
4
+2x），x∈R．
（1）求函数的最大、最小值；
（2）求函数的最小正周期；
（3）求函数的单调区间；
（4）函数的图象可由函数y=
2
2
cos（2x-
π
2
），x∈R的图象经过怎样的变换得到？
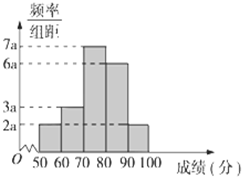某校为了了解学生的数学学习情况，以5%的比例随机抽取20位学生，根据他们的期中考试数学成绩作出频率分布直方图如右图所示，其中成绩分组区间是：[50，60）、[60，70）、[70，80）、[80，90）、[90，100），
（Ⅰ）求图中a的值，并根据频率分布直方图估计该校成绩落在[50，60）中的学生人数；
（Ⅱ）从样本中成绩在[50，70）的学生中人任选2人，求这2人的成绩都在[60，70）中的概率．
执行如图的程序框图，若p=5，则输出的S值为（　　）
A、
63
64
B、
15
16
C、
7
8
D、
31
32
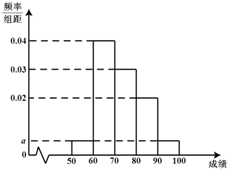某校为了了解学生数学学习情况，随机抽取60位学生期中考试数学成绩，并作出频率分布直方图如图所示，其中成绩分组区间是：[50，60）、[60，70）、[70，80）、[80，90）、[90，100），
（Ⅰ）求图中a的值，并根据频率分布直方图估计该校学生数学成绩的平均分；
（Ⅱ）若这60名学生的数学成绩某些分数段的人数（x）与语文成绩相应分数段的人数（y）之比如下表所示，求语文成绩在[50，90）之外的人数．
分数段[50，60）[60，70）[70，80）[80，90）
x：y1：12：13：44：5
计算：（1）tanα=2，求cosα2+sin（π+α）cos（-α）．
（2）若cosα+sinα=
1
5
，且α为第二象限角，求tanα．
（3）若cos（α+
π
3
）=
3
5
且α为第四象限角，求cosα．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网