题目内容
12.设△AnBnCn为一族一边长始终相等的三角形,角An,Bn,Cn的对边分别为an,bn,cn(n∈N*),满足b1+c1=2a1,an+1=an,且an,bn+1,cn与an,cn+1,bn分别成等差数列,则角An的最大值是( )| A. | $\frac{5π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
分析 运用等差数列的中项的性质,可得an+cn=2bn+1,an+bn=2cn+1,推得bn+cn=2a1,再由余弦定理和基本不等式可得
角An的最大值.
解答 解:由b1+c1=2a1,an+1=an,
且an,bn+1,cn与an,cn+1,bn分别成等差数列,
可得an+cn=2bn+1,an+bn=2cn+1,
即有a1+c1=2b2,a1+b1=2c2,
相加可得2a1+b1+c1=2(b2+c2),
即为b2+c2=2a1,
同理可得bn+cn=2a1,
由余弦定理可得,cosAn=$\frac{{{b}_{n}}^{2}+{{c}_{n}}^{2}-{{a}_{n}}^{2}}{2{b}_{n}{c}_{n}}$
=$\frac{({b}_{n}+{c}_{n})^{2}-{{a}_{1}}^{2}-2{b}_{n}{c}_{n}}{2{b}_{n}{c}_{n}}$=$\frac{3{{a}_{1}}^{2}}{2{b}_{n}{c}_{n}}$-1,
由bn+cn=2a1≥2$\sqrt{{b}_{n}{c}_{n}}$,
即为a12≥bncn,(当且仅当bn=cn取得等号),
则有cosAn≥$\frac{3}{2}$-1=$\frac{1}{2}$,
即有An≤$\frac{π}{3}$.
则角An的最大值是$\frac{π}{3}$.
故选:C.
点评 本题考查等差数列的中项的性质,考查余弦定理和基本不等式的运用,属于中档题.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
17.化简log2$\sqrt{2\sqrt{2\sqrt{2\sqrt{2}…\sqrt{2}}}}$(总共有2015个2)的结果为( )
| A. | $\frac{2014}{2015}$ | B. | $\frac{{2}^{2015}-1}{{2}^{2015}}$ | C. | $\frac{{2}^{2014}-1}{{2}^{2014}}$ | D. | $\frac{{2}^{2016}-1}{{2}^{2016}}$ |
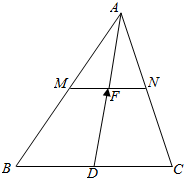 在△ABC中,已知A(7,8),B(3,5),C(4,3),M,N,D分别是AB,AC,BC的中点,且MN与AD交于点F,求$\overrightarrow{DF}$的坐标.
在△ABC中,已知A(7,8),B(3,5),C(4,3),M,N,D分别是AB,AC,BC的中点,且MN与AD交于点F,求$\overrightarrow{DF}$的坐标.