题目内容
4.如果A(1,-2)、B(4,a)、C(-2,a-1)在同一条直线上,求a的值.分析 三点A,B,C共线,可得kAB=kAC,即可得出.
解答 解:kAB=$\frac{a+2}{3}$,kAC=$\frac{a+1}{-3}$,
∵三点A,B,C共线,
∴kAB=kAC,
∴$\frac{a+2}{3}$=$\frac{a+1}{-3}$,
解得a=-$\frac{3}{2}$.
点评 本题考查了三点共线与斜率的关系,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
14.实数x,y满足不等式组$\left\{\begin{array}{l}{x-y+2≥0}\\{2x-y-5≤0}\\{x+y-4≥0}\end{array}\right.$,则z=|x+2y-4|的最大值为( )
| A. | 21 | B. | 20 | C. | 25 | D. | 23 |
12.设△AnBnCn为一族一边长始终相等的三角形,角An,Bn,Cn的对边分别为an,bn,cn(n∈N*),满足b1+c1=2a1,an+1=an,且an,bn+1,cn与an,cn+1,bn分别成等差数列,则角An的最大值是( )
| A. | $\frac{5π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
9.已知公比为q的等比数列{an},且满足条件|q|>1,a2+a7=2,a4a5=-15,则a12=( )
| A. | -$\frac{27}{25}$ | B. | -$\frac{25}{3}$ | C. | -$\frac{27}{25}$或-$\frac{25}{3}$ | D. | $\frac{25}{3}$ |
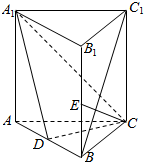 如图,直三棱柱ABC-A1B1C1中,D、E分别是AB、BB1的中点.
如图,直三棱柱ABC-A1B1C1中,D、E分别是AB、BB1的中点.