题目内容
1．在等差数列{an}中，已知a1=2，a7=14，求a12和S5的值．分析 利用等差数列的通项公式及其前n项和公式即可得出．
解答 解：设等差数列{an}的公差为d，∵a1=2，a7=14，
∴2+6d=14，解得d=2．
∴an=2+2（n-1）=2n．
∴a12=24．
S5=$\frac{5×（2+10）}{2}$=30．
点评 本题考查了等差数列的通项公式及其前n项和公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
如图所示，三棱锥P-ABC中，∠ABC为直角，PB⊥平面ABC，AB=BC=PB=1，M为PC的中点，N为AC中点，以{$\overrightarrow{BA}$，$\overrightarrow{BC}$，$\overrightarrow{BP}$}为基底，则$\overrightarrow{MN}$的坐标为$（\frac{1}{2}，0，-\frac{1}{2}）$．
12．设△AnBnCn为一族一边长始终相等的三角形，角An，Bn，Cn的对边分别为an，bn，cn（n∈N*），满足b1+c1=2a1，an+1=an，且an，bn+1，cn与an，cn+1，bn分别成等差数列，则角An的最大值是（ ）
| A． | $\frac{5π}{6}$ | B． | $\frac{2π}{3}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{6}$ |
9．已知公比为q的等比数列{an}，且满足条件|q|＞1，a2+a7=2，a4a5=-15，则a12=（ ）
| A． | -$\frac{27}{25}$ | B． | -$\frac{25}{3}$ | C． | -$\frac{27}{25}$或-$\frac{25}{3}$ | D． | $\frac{25}{3}$ |
6．已知向量$\overrightarrow{a}$=（1，2），则|$\overrightarrow{a}$|=（ ）
| A． | 3 | B． | $\sqrt{3}$ | C． | 5 | D． | $\sqrt{5}$ |
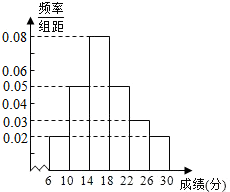某省去年高三200000考生英语听力考试成绩服从正态分布N（17，9），现从某校高三年级随机抽取50名考生的成绩，发现全部介于[6，30]之间，将成绩按如下方式分成6组：第1组[6，10），第2组[10，14），…，第6组[26，30]，如图是按上述分组方法得到的频率分布直方图．