题目内容
6.已知线段AB的长度是10,它的两个端点分别在x轴、y轴上滑动,则AB的中点P的轨迹方程是x2+y2=25.分析 由两点间距离公式表示出|AB|,再利用中点坐标公式建立线段AB的中点与其两端点的坐标关系,最后代入整理即可.
解答 解:设A(m,0)、B(0,n),则|AB|2=m2+n2=100,
再设线段AB中点P的坐标为(x,y),则x=$\frac{m}{2}$,y=$\frac{n}{2}$,即m=2x,n=2y,
所以4x2+4y2=100,即AB中点的轨迹方程为x2+y2=25.
故答案为:x2+y2=25.
点评 本题考查点轨迹方程的求法,考查两点间距离公式、中点坐标公式及方程思想.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
16.边长为5,7,8的三角形的最大角与最小角的和为( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{5π}{6}$ |
15.已知向量$\overrightarrow{a}$=(1,1),|$\overrightarrow{OM}$|=1,$\overrightarrow{ON}$•$\overrightarrow{a}$=2,其中O为坐标原点,那么$\overrightarrow{MN}$•$\overrightarrow{a}$的最小值为( )
| A. | $\sqrt{2}$-1 | B. | $\sqrt{2}$ | C. | 2-$\sqrt{2}$ | D. | 2 |
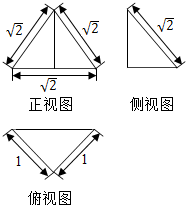 如图所示为一个几何体的三视图:
如图所示为一个几何体的三视图: