题目内容
已知函数f（x）=4cosxsin（x+
）-1．
（1）求f（x）在区间[-
，
]上的最大值和最小值及此时的x的值；
（2）若f（α）=
，求sin（
-4α）．
| π |
| 6 |
（1）求f（x）在区间[-
| π |
| 6 |
| π |
| 4 |
（2）若f（α）=
| 1 |
| 2 |
| π |
| 6 |
考点：三角函数的最值
专题：三角函数的求值
分析：（1）化简可得f（x）=2sin（2x+
），由x∈[-
，
]结合三角函数的最值可得；
（2）由题意可得sin（2α+
）=
，由诱导公式和二倍角公式可得sin（
-4α）=1-2sin2（2α+
），代值计算可得．
| π |
| 6 |
| π |
| 6 |
| π |
| 4 |
（2）由题意可得sin（2α+
| π |
| 6 |
| 1 |
| 4 |
| π |
| 6 |
| π |
| 6 |
解答：
解：（1）化简可得f（x）=4cosxsin（x+
）-1
=4cosx（
sinx+
cosx）-1
=
sin2x+cos2x=2sin（2x+
），
∵x∈[-
，
]，
∴当x=-
时，f（x）取最小值-1，
当x=
时，f（x）取最大值2；
（2）由题意f（α）=2sin（2α+
）=
，
∴sin（2α+
）=
，
∴sin（
-4α）=sin[
-（4α+
）]
=cos（4α+
）=1-2sin2（2α+
）=
| π |
| 6 |
=4cosx（
| ||
| 2 |
| 1 |
| 2 |
=
| 3 |
| π |
| 6 |
∵x∈[-
| π |
| 6 |
| π |
| 4 |
∴当x=-
| π |
| 6 |
当x=
| π |
| 6 |
（2）由题意f（α）=2sin（2α+
| π |
| 6 |
| 1 |
| 2 |
∴sin（2α+
| π |
| 6 |
| 1 |
| 4 |
∴sin（
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
=cos（4α+
| π |
| 3 |
| π |
| 6 |
| 7 |
| 8 |
点评：本题考查三角函数的最值，涉及三角函数公式的应用和诱导公式，属基础题．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
已知全集U=R，集合 A={x|0≤x≤2}，B={x|x2-x＞0}，则图中的阴影部分表示的集合为（ ）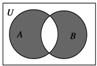
| A、（-∞，1]U（2，+∞） |
| B、（-∞，0）∪（1，2） |
| C、[1，2） |
| D、（1，2] |