题目内容
16．已知$\overrightarrow a=（2，-1，x），\overrightarrow b=（3，2，-1）$，若$\overrightarrow a⊥\overrightarrow b$则实数x=4．分析 利用向量垂直的性质求解．
解答 解：∵$\overrightarrow a=（2，-1，x），\overrightarrow b=（3，2，-1）$，$\overrightarrow a⊥\overrightarrow b$，
∴$\overrightarrow{a}•\overrightarrow{b}$=6-2-x=0，
解得x=4．
∴实数x的值为4．
故答案为：4．
点评 本题考查实数值的求法，是基础题，解题时要认真审题，注意向量垂直的性质的合理运用．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
7．设抛物线C：y2=8x的焦点为F，过F的直线与C相交于A，B两点，记点F到直线l：x=-2的距离为d，则有（ ）
| A． | |AB|=2d | B． | |AB|≥2d | C． | |AB|≤2d | D． | |AB|＜2d |
11．已知正方体ABCD-A′B′C′D′，点E是A′C′的中点，点F是AE的三等分点，且$AF=\frac{1}{2}EF$，则$\overrightarrow{AF}$等于（ ）
| A． | $\overrightarrow{AA′}$+$\frac{1}{2}$$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AD}$ | B． | $\frac{1}{2}$$\overrightarrow{AA′}$+$\frac{1}{2}$$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AD}$ | C． | $\frac{1}{2}$$\overrightarrow{AA′}$+$\frac{1}{6}$$\overrightarrow{AB}$+$\frac{1}{6}$$\overrightarrow{AD}$ | D． | $\frac{1}{3}$$\overrightarrow{AA′}$+$\frac{1}{6}$$\overrightarrow{AB}$+$\frac{1}{6}$$\overrightarrow{AD}$ |
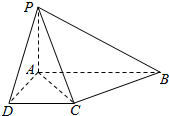如图，已知四棱锥P-ABCD的底面为直角梯形，AB∥CD，∠DAB=90°，PA⊥底面ABCD，且PA=AD=DC=$\frac{1}{2}$AB=1．
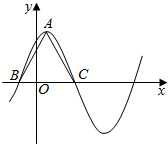函数$f（x）=6{cos^2}\frac{ωx}{2}+\sqrt{3}sinωx-3（{ω＞0}）$在一个周期内的图象如图所示，A为图象的最高点，B、C为图象与x轴的交点，且△ABC为正三角形．