题目内容
6.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象在y轴上的截距为1,在相邻两最值点(x0,2)(x0+$\frac{3}{2}$,-2)(x0>0)上分别取得最大值和最小值.(1)求f(x)的解析式;
(2)求方程f(x)=a(1<a<2),在[0,9]内的所有实数根之和.
分析 (1)由题意得f(0)=1,f(x)的最大值等于2,周期的一半等于$\frac{3}{2}$,列出方程组解出A,ω,φ,
(2)作出f(x)的函数图象可发现所有的实根都两两关于对称轴对称,根据对称的性质得出实数根的和.
解答 解:(1)∵f(x)在相邻两最值点(x0,2),(x0+$\frac{3}{2}$,-2)(x0>0)上分别取得最大值和最小值,
∴A=2,$\frac{2π}{ω}$×$\frac{1}{2}$=$\frac{3}{2}$,解得ω=$\frac{2}{3}$π,
∵f(x)的图象在y轴上的截距为1,∴f(0)=2sinφ=1,sinφ=$\frac{1}{2}$.∵|φ|<$\frac{π}{2}$,∴φ=$\frac{π}{6}$.
∴f(x)=2sin($\frac{2π}{3}$x+$\frac{π}{6}$).
(2)∵作出f(x)的函数图象如图所示: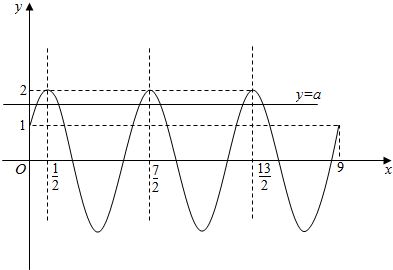
由图象可知当1<a<2时,y=a与f(x)图象有6个交点,他们分别关于f(x)的三条对称轴对称,
∴f(x)=a在[0,9]内的所有实根之和等于$\frac{1}{2}×2$+$\frac{7}{2}×2$+$\frac{13}{2}$×2=21.
点评 本题考查了三角函数解析式的求解,三角函数的图象与性质,作出函数图象是解题关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
11.若关于x的不等式xlnx+x-kx+3k>0对任意x>1恒成立,则整数k的最大值是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
15.已知函数f(x)=sin(2x+θ)-$\sqrt{3}$cos(2x+θ)(|θ|<$\frac{π}{2}$)的图象关于原点对称,则y=f(x)在下列哪个区间上是减函数( )
| A. | (0,$\frac{π}{2}$) | B. | ($\frac{π}{2}$,π) | C. | ($\frac{π}{4}$,$\frac{π}{2}$) | D. | (-$\frac{π}{4}$,$\frac{π}{4}$) |
16.已知随机变量X:B(20,$\frac{1}{3}$),要使P(X=k)的值最大,则k=( )
| A. | 5或6 | B. | 6或7 | C. | 7 | D. | 7或8 |
