题目内容
4.已知P是抛物线C:x2=4y上一动点,直线l:y=x-2.(1)求点P到直线l的最小距离;
(2)当P到直线l的距离最小时,求以点P为圆心且与抛物线C准线相切的圆方程.
分析 (1)先设直线y=x+t是抛物线的切线,最小距离是两直线之间的距离;
(2)求出抛物线C的准线,可得半径,即可求以点P为圆心且与抛物线C的准线相切的圆的方程.
解答 解:(1)设直线y=x+t是抛物线的切线,所求最小距离是两直线之间的距离,
代入化简得x2-4x-4t=0
由△=0得t=-1
代入方程得x=2,y=1,
∴P为(2,1),
∴点P到直线l的最小距离为=$\frac{|2-1-2|}{\sqrt{2}}$=$\sqrt{2}$;
(2)抛物线C:x2=4y的准线为y=-1,
∵圆以点P为圆心且与抛物线C的准线相切,
∴半径为2,
∴圆的方程为(x-2)2+(y-1)2=4.
点评 本题主要考查抛物线的应用和抛物线与直线的关系.考查了学生综合分析和解决问题的能力.

练习册系列答案
相关题目
14.已知命题p:?x≥0,2x≥1;命题q:若x>y,则x2>y2.则下列命题为真命题的是( )
| A. | p∧q | B. | p∧¬q | C. | ¬p∧¬q | D. | ¬p∨q |
19.命题“?x∈R,x2+2x+2>0”的否定是( )
| A. | ?x∈R,x2+2x+2≤0 | B. | ?x∈R,x2+2x+2≤0 | C. | ?x∈R,x2+2x+2<0 | D. | ?x∈R,x2+2x+2>0 |
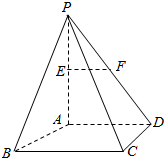 如图,四棱锥P-ABCD底面是正方形,PA⊥底面ABCD,E,F分别为PA,PD中点.
如图,四棱锥P-ABCD底面是正方形,PA⊥底面ABCD,E,F分别为PA,PD中点.