题目内容
1.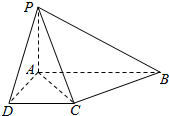 如图,已知四棱锥P-ABCD的底面为直角梯形,AB∥CD,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=$\frac{1}{2}$AB=1.
如图,已知四棱锥P-ABCD的底面为直角梯形,AB∥CD,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=$\frac{1}{2}$AB=1.(1)求证:平面PAD⊥平面PCD;
(2)求直线AC与直线PB所成角的余弦值.
分析 (1)由底面为直角梯形可得CD⊥AD,由PA⊥底面ABCD可得PA⊥CD,故而CD⊥平面PAD,推出平面PAD⊥平面PCD;
(2)建立空间直角坐标系,求出$\overrightarrow{AC},\overrightarrow{PB}$的坐标,代入向量的夹角公式计算异面直线所成的角.
解答 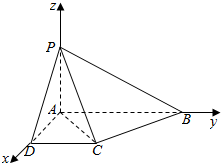 证明:(1)∵AB∥CD,∠DAB=90°,∴CD⊥AD,
证明:(1)∵AB∥CD,∠DAB=90°,∴CD⊥AD,
∵PA⊥平面ABCD,CD?平面ABCD,
∴PA⊥CD,又∵PA?平面PAD,AD?平面PAD,AD∩PA=A,
∴CD⊥平面PAD,∵CD?平面ACD,
∴平面PAD⊥平面PCD.
(2)建立如图所示的空间直角坐标系,则A(0,0,0),B(0,2,0),C(1,1,0),P(0,0,1).
∴$\overrightarrow{AC}$=(1,1,0),$\overrightarrow{PB}$=(0,2,-1),∴$\overrightarrow{AC}•\overrightarrow{PB}$=2,|$\overrightarrow{AC}$|=$\sqrt{2}$,|$\overrightarrow{PB}$|=$\sqrt{5}$,
∴cos<$\overrightarrow{AC},\overrightarrow{PB}$>=$\frac{\overrightarrow{AC}•\overrightarrow{PB}}{|\overrightarrow{AC}|•|\overrightarrow{PB}|}$=$\frac{\sqrt{10}}{5}$.
∴直线AC与直线PB所成角的余弦值为$\frac{\sqrt{10}}{5}$.
点评 本题考查了面面垂直的判定,异面直线所成角的计算,常用向量法来解决空间角的计算问题.

| A. | [0,1)∪(1,2] | B. | [0,1)∪(1,4] | C. | [0,1) | D. | (1,4] |
| A. | 60° | B. | 30° | C. | 150° | D. | 120° |
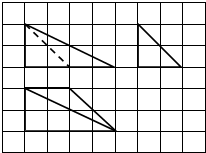
| A. | 2 cm3 | B. | 4 cm3 | C. | 6 cm3 | D. | 8 cm3 |
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
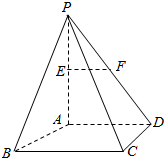 如图,四棱锥P-ABCD底面是正方形,PA⊥底面ABCD,E,F分别为PA,PD中点.
如图,四棱锥P-ABCD底面是正方形,PA⊥底面ABCD,E,F分别为PA,PD中点.