题目内容
7.设抛物线C:y2=8x的焦点为F,过F的直线与C相交于A,B两点,记点F到直线l:x=-2的距离为d,则有( )| A. | |AB|=2d | B. | |AB|≥2d | C. | |AB|≤2d | D. | |AB|<2d |
分析 由抛物线方程求出F的坐标,得到F到准线l的距离d=4,设出过焦点的直线方程,和抛物线联立后利用根与系数的关系求出焦点弦的长度,然后核对四个选项得答案.
解答  解:如图,设A(x1,y1),B(x2,y2),
解:如图,设A(x1,y1),B(x2,y2),
由抛物线W:y2=8x,得焦点为F(2,0),准线l:x=-2.
F到准线的距离d=4.
设直线AB的方程为x=ty+2,
联立抛物线方程,得y1+y2=8t.
x1+x2=t(y1+y2)+4=8t2+4≥4.
则|AB|=x1+x2+4≥8=2d.
故选:B.
点评 本题考查了抛物线的简单几何性质,考查了数学转化思想方法,是中档题.

练习册系列答案
相关题目
18.设Sn为等差数列{an}的前n项和,且a1+a10-a5=6,则S11=( )
| A. | 55 | B. | 66 | C. | 110 | D. | 132 |
19.命题“?x∈R,x2+2x+2>0”的否定是( )
| A. | ?x∈R,x2+2x+2≤0 | B. | ?x∈R,x2+2x+2≤0 | C. | ?x∈R,x2+2x+2<0 | D. | ?x∈R,x2+2x+2>0 |
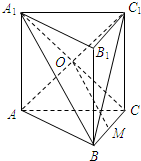 如图,已知直三棱柱ABC-A1B1C1的侧面ACC1A1是正方形,点O是侧面ACC1A1的中心,∠ACB=$\frac{π}{2}$,M是棱BC的中点.
如图,已知直三棱柱ABC-A1B1C1的侧面ACC1A1是正方形,点O是侧面ACC1A1的中心,∠ACB=$\frac{π}{2}$,M是棱BC的中点.