题目内容
14.若点P在y=x2上,点Q在x2+(y-3)2=1上,则|PQ|的最小值为( )| A. | $\sqrt{3}$-1 | B. | $\frac{\sqrt{11}}{2}$-1 | C. | 2 | D. | $\frac{\sqrt{10}}{2}$-1 |
分析 求得圆心圆心A(0,3),半径为1,设P(x,x2),丨PQ丨=丨AP丨-丨AQ丨=$\sqrt{{x}^{2}+({x}^{2}-3)^{2}}-1$=$\sqrt{({x}^{2}-\frac{5}{2})^{2}+\frac{11}{4}}$,由二次的性质即可求得|PQ|的最小值.
解答 解:圆x2+(y-3)2=1的圆心A(0,3),半径为1,
∵点P在抛物线y=x2上,设P(x,x2),
∴丨PQ丨=丨AP丨-丨AQ丨=$\sqrt{{x}^{2}+({x}^{2}-3)^{2}}-1$=$\sqrt{{x}^{4}-5{x}^{2}+9}$-1=$\sqrt{({x}^{2}-\frac{5}{2})^{2}+\frac{11}{4}}$,
由二次函数的性质可知:当x2=$\frac{5}{2}$时,丨PQ丨取最小值,最小值为:$\frac{\sqrt{11}}{2}$-1,
故选B.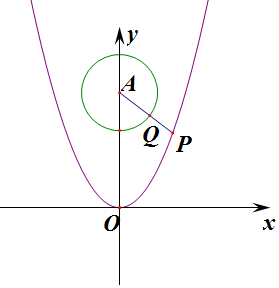
点评 本题考查圆的方程与抛物线的应用,考查二次函数的性质的应用,属于中档题.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
5.已知函数f(x)=x2+2x-a与g(x)=2x+2lnx($\frac{1}{e}$≤x≤e)的图象有两个不同的交点,则实数a的取值范围是( )
| A. | (1,$\frac{1}{{e}^{2}}$+2] | B. | [$\frac{1}{{e}^{2}}$+2,e2-2] | C. | (1,e2-2] | D. | [e2-2,+∞) |
9.设函数f(x)=alnx-bx2(x>0),若函数y=f(x)在x=1处与直线y=-1相切.
(Ⅰ) 求实数a,b的值;
(Ⅱ) 求函数y=f(x)在$[{\frac{1}{e},e}]$上的最大值.
(Ⅰ) 求实数a,b的值;
(Ⅱ) 求函数y=f(x)在$[{\frac{1}{e},e}]$上的最大值.
19.已知向量$\overrightarrow a=(2k-3,-6)$,$\overrightarrow b=(2,1)$,且$\overrightarrow a⊥\overrightarrow b$,则实数k的值为( )
| A. | 2 | B. | -2 | C. | 3 | D. | -3 |
6.向面积为S的平行四边形ABCD中任投一点M,则△MCD的面积小于$\frac{S}{3}$的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
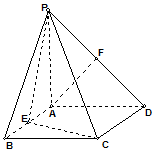 如图,四棱锥P-ABCD的底面是矩形,PA⊥底面ABCD,PA=AD,点E、F分别为棱AB、PD的中点.
如图,四棱锥P-ABCD的底面是矩形,PA⊥底面ABCD,PA=AD,点E、F分别为棱AB、PD的中点.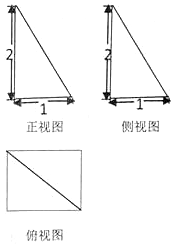 已知四棱锥P-ABCD,PA⊥底面ABCD,其三视图如下,若M是PD的中点.
已知四棱锥P-ABCD,PA⊥底面ABCD,其三视图如下,若M是PD的中点.