题目内容
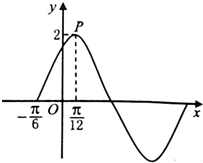已知函数f（x）=Asin（ωx+φ）（ω＞0，A＞0，φ∈（0，| π |
| 2 |
（1）求函数f（x）的解析式；
（2）求函数f（-x）的单调增区间；
（3）求函数图象的对称中心和对称轴；
（4）解不等式f（x）≥
| 3 |
（5）函数f（x）的图象可由y=sinx的图象经过怎样变换得到？
考点：由y=Asin（ωx+φ）的部分图象确定其解析式,正弦函数的图象,函数y=Asin（ωx+φ）的图象变换
专题：综合题,三角函数的图像与性质
分析：（1）利用最高点可求A，利用周期求出ω，（
，2）代入，求出φ，可得函数f（x）的解析式；
（2）令-2x+
∈[2kπ-
，2kπ+
]，求函数f（-x）的单调增区间；
（3）利用正弦函数的对称中心和对称轴，求函数图象的对称中心和对称轴；
（4）由f（x）≥
，可得2sin（2x+
）≥
，即可解不等式f（x）≥
；
（5）利用函数的图象变换规律，可得结论．
| π |
| 12 |
（2）令-2x+
| π |
| 3 |
| π |
| 2 |
| π |
| 2 |
（3）利用正弦函数的对称中心和对称轴，求函数图象的对称中心和对称轴；
（4）由f（x）≥
| 3 |
| π |
| 3 |
| 3 |
| 3 |
（5）利用函数的图象变换规律，可得结论．
解答：
解：（1）由题意，A=2，T=4（
+
）=π，
∴ω=2，
∴f（x）=2sin（2x+φ），
（
，2）代入可得sin（
+φ）=1，φ∈（0，
），∴φ=
，
∴f（x）=2sin（2x+
）；
（2）f（-x）=-2sin（2x-
），
令2x-
∈[2kπ+
，2kπ+
]，可得函数f（-x）的单调增区间为[kπ+
，kπ+
π]，k∈Z；
（3）由2x+
=kπ，可得x=
-
，故函数图象的对称中心为（
-
，0），k∈Z；
由2x+
=kπ+
，可得x=
+
，故函数图象的对称轴为x=
+
，k∈Z；
（4）由f（x）≥
，可得2sin（2x+
）≥
，解得2kπ+
≤2x+
≤2kπ+
∴不等式的解集为{x|kπ≤x≤kπ+
，k∈Z}；
（5）函数f（x）的图象可由y=sinx的图象向左平移
个单位，再将横坐标变为原来的一半，纵坐标变为原来的2倍．
| π |
| 12 |
| π |
| 6 |
∴ω=2，
∴f（x）=2sin（2x+φ），
（
| π |
| 12 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
∴f（x）=2sin（2x+
| π |
| 3 |
（2）f（-x）=-2sin（2x-
| π |
| 3 |
令2x-
| π |
| 3 |
| π |
| 2 |
| 3π |
| 2 |
| π |
| 12 |
| 7 |
| 12 |
（3）由2x+
| π |
| 3 |
| kπ |
| 2 |
| π |
| 6 |
| kπ |
| 2 |
| π |
| 6 |
由2x+
| π |
| 3 |
| π |
| 2 |
| kπ |
| 2 |
| π |
| 12 |
| kπ |
| 2 |
| π |
| 12 |
（4）由f（x）≥
| 3 |
| π |
| 3 |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
∴不等式的解集为{x|kπ≤x≤kπ+
| π |
| 6 |
（5）函数f（x）的图象可由y=sinx的图象向左平移
| π |
| 3 |
点评：本题考查三角函数的图象与性质，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
五位同学参加某作家的签字售书活动，则甲、乙都排在丙前面的方法有（ ）
| A、20种 | B、24种 |
| C、40种 | D、56种 |
已知两条直线l1：x+y-2=0，l2：3x+ay+2=0，且l1⊥l2，则a=（ ）
A、-
| ||
| B、-3 | ||
C、
| ||
| D、3 |
若直线ax+2y+1=0与直线x+y-2=0互相垂直，那么a的值等于（ ）
| A、1 | ||
B、-
| ||
C、-
| ||
| D、-2 |
已知一个算法的流程图如图所示，则输出的结果是（ ）
| A、2 | B、5 | C、25 | D、26 |