题目内容
在△ABC中,角A,B,C的对边分别为a,b,c,满足asinAsinB+bcos2A=
a,
•
=a2
(1)求角C的大小;
(2)若c=2
,求△ABC的面积S.
| 2 |
| CA |
| CB |
(1)求角C的大小;
(2)若c=2
| 2 |
考点:正弦定理,余弦定理
专题:解三角形
分析:(1)利用正弦定理把已知等式中边,转化为角的正弦化简整理求得a和b的关系式,进而根据已知
•
=a2,利用向量的数量积公式求得cosC的值,进而求得C.
(2)利用余弦定理和(1)中a和b的关系求得a和b,进而利用三角形面积公式求得答案.
| CA |
| CB |
(2)利用余弦定理和(1)中a和b的关系求得a和b,进而利用三角形面积公式求得答案.
解答:
解:(1)由正弦定理有sin2AsinB+sinBcos2A=
sinA,
∴sinB=
sinA,
∴b=
a,
•
=bacosC=a2
∴cosC=
,
∴C=
(2)由余弦定理有c2=a2+b2-2abcosC=a2+2a2-2a
a•
=a2,
∴a=c=2
,b=
a=4,
∴S=
absinC=
×2
×4×
=4.
| 2 |
∴sinB=
| 2 |
∴b=
| 2 |
| CA |
| CB |
∴cosC=
| ||
| 2 |
∴C=
| π |
| 4 |
(2)由余弦定理有c2=a2+b2-2abcosC=a2+2a2-2a
| 2 |
| ||
| 2 |
∴a=c=2
| 2 |
| 2 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
点评:本题主要考查了三角函数恒等变换的应用,解三角形问题,向量的数量积公式的应用.注重了对学生基础公式灵活运用的考查.

练习册系列答案
相关题目
已知函数f(x)=
,若关于x的方程f(x)=k有3个不同的实根,则实数k的取值范围为( )
|
| A、[1,+∞) |
| B、(0,+∞) |
| C、(0,2) |
| D、(1,2] |
sin(-600°)的值是( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
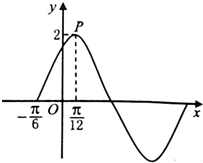 已知函数f(x)=Asin(ωx+φ)(ω>0,A>0,φ∈(0,
已知函数f(x)=Asin(ωx+φ)(ω>0,A>0,φ∈(0, 如图,有一个算法流程图.在集合A={x∈R|-10≤x≤10}中随机地取一个数值做为x输入,则输出的y值落在区间(-5,3)内的概率值为
如图,有一个算法流程图.在集合A={x∈R|-10≤x≤10}中随机地取一个数值做为x输入,则输出的y值落在区间(-5,3)内的概率值为