题目内容
若直线ax+2y+1=0与直线x+y-2=0互相垂直,那么a的值等于( )
| A、1 | ||
B、-
| ||
C、-
| ||
| D、-2 |
考点:直线的一般式方程与直线的垂直关系
专题:直线与圆
分析:利用相互垂直的直线斜率之间的关系即可得出.
解答:
解:直线ax+2y+1=0的斜率k1=-
,直线x+y-2=0的斜率k2=-1.
∵直线ax+2y+1=0与直线x+y-2=0互相垂直,
∴k1•k2=-1.
∴-
×(-1)=-1,
解得a=-2.
故选:D.
| a |
| 2 |
∵直线ax+2y+1=0与直线x+y-2=0互相垂直,
∴k1•k2=-1.
∴-
| a |
| 2 |
解得a=-2.
故选:D.
点评:本题考查了相互垂直的直线斜率之间的关系,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在平行四边形ABCD中,AC与BD交于点M,则
+
=( )
| AB |
| CM |
A、
| ||
B、
| ||
C、
| ||
D、
|
sin(-600°)的值是( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
若函数f(x)=
,则f(2)+f(
)= ,记f(1)+f(2)+f(4)+f(8)+…+f(1024)=m,f(
)+f(
)+f(
)+…+f(
)=n,则m+n= .
| x+3 |
| x+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 1024 |
已知a=
,函数f(x)=ax,若实数m,n满足f(m)>f(n),则m、n满足的关系为( )
| ||
| 2 |
| A、m+n<0 | B、m+n>0 |
| C、m>n | D、m<n |
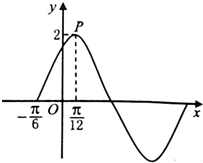 已知函数f(x)=Asin(ωx+φ)(ω>0,A>0,φ∈(0,
已知函数f(x)=Asin(ωx+φ)(ω>0,A>0,φ∈(0,