题目内容
设a＞0且a≠1，函数y=a2x+2ax+1在[-1，1]的最大值是14，求a的值．
考点：指数函数综合题
专题：函数的性质及应用
分析：令t=ax（a＞0，a≠1），则原函数化为y=t2+2t-1=（t+1）2-2（t＞0），分类①当0＜a＜1时，②当a＞1时，利用单调性求解即可．
解答：
解：令t=ax（a＞0，a≠1），则原函数化为y=t2+2t-1=（t+1）2-2（t＞0）
①当0＜a＜1时，x∈[-1，1]，t=ax∈[a，
]，
此时f（x）在[a，
]上为增函数，所以f（x）max=f（
）=（
+1）2-2=1
所以a=-
（舍去）或a=
，
，x∈[-1，1]，t=ax∈[a，
]，此时f（t）在[
，a]上为增函数，所以f（x）max=f（a）=（a+1）2-2=14，
所以a=-5（舍去）或a=3，
综上a=
或a=3．
①当0＜a＜1时，x∈[-1，1]，t=ax∈[a，
| 1 |
| a |
此时f（x）在[a，
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
所以a=-
| 1 |
| 5 |
| 1 |
| 3 |
，x∈[-1，1]，t=ax∈[a，
| 1 |
| a |
| 1 |
| a |
所以a=-5（舍去）或a=3，
综上a=
| 1 |
| 3 |
点评：本题考查了指数函数的性质的应用，难度较大，属于中档题，注意复合函数的单调性的运用．
练习册系列答案
相关题目
已知函数f（x）=
，若关于x的方程f（x）=k有3个不同的实根，则实数k的取值范围为（ ）
|
| A、[1，+∞） |
| B、（0，+∞） |
| C、（0，2） |
| D、（1，2] |
已知命题p：?x∈R，x＞2x，命题q：?x∈R，x2＞0，则（ ）
| A、命题p∨q是假命题 |
| B、命题p∧q是真命题 |
| C、命题p∧（￢q）是真命题 |
| D、命题p∨（￢q）是假命题 |
在平行四边形ABCD中，AC与BD交于点M，则
+
=（ ）
| AB |
| CM |
A、
| ||
B、
| ||
C、
| ||
D、
|
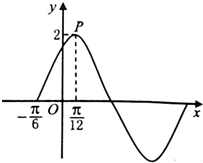已知函数f（x）=Asin（ωx+φ）（ω＞0，A＞0，φ∈（0，