题目内容
已知函数f(x)=ln(x+1)+ax2-x,a∈R.
(Ⅰ)当a=
时,求函数y=f(x)的极值;
(Ⅱ)是否存在实数b∈(1,2),使得当x∈(-1,b]时,函数f(x)的最大值为f(b)?若存在,求实数a的取值范围,若不存在,请说明理由.
(Ⅰ)当a=
| 1 |
| 4 |
(Ⅱ)是否存在实数b∈(1,2),使得当x∈(-1,b]时,函数f(x)的最大值为f(b)?若存在,求实数a的取值范围,若不存在,请说明理由.
考点:利用导数研究函数的单调性,利用导数研究函数的极值,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(Ⅰ)将a=
代入到f(x)的表达式中并求导,计算其单调区间从而确定其极值.
(Ⅱ)f′(x)=
,注意到分子中x前的系数为2a,则分成a≤0和a>0两种情况讨论.其中,当a>0时,f′(x)=
,(x>-1)再分成
-1>0和
-1<0两种情况分别讨论计算.
| 1 |
| 4 |
(Ⅱ)f′(x)=
| x(2ax-(1-2a)) |
| x+1 |
2ax(x-(
| ||
| x+1 |
| 1 |
| 2a |
| 1 |
| 2a |
解答:
解:(Ⅰ)当a=
时,f(x)=ln(x+1)+
x2-x,
则f′(x)=
+
x-1,化简得f′(x)=
,(x>-1)
∴函数在(-1,0),(1,+∞)上单调递增,在(0,1)上单调递减,且f(0)=0,f(1)=ln2-
,
∴函数y=f(x)在x=1处取到极小值为ln2-
,在x=0处取到极大值为0.
(Ⅱ)由题意f′(x)=
,
(1)当a≤0时,函数f(x)在(-1,0)上单调递增,在(0,+∞)上单调递减,
此时,不存在实数b∈(1,2)使得当x∈(-1,b]时,函数f(x)的最大值为f(b);
(2)当a>0时,令f′(x)=0,有x=0或x=
-1,
①当a=
时,函数f(x)在(-1,+∞)上单调递增,显然符合题意;
②当
-1>0即0<a<
时,函数f(x)在(-1,0)和(
-1,+∞)上单调递增,在(0,
-1)上单调递减,
此时由题,只需f(1)>0,解得a>1-ln2,又1-ln2<
,
∴此时实数a的取值范围是1-ln2<a<
③当
-1<0即a>
时,函数f(x)在(-1,
-1)和(0,+∞)上单调递增,在(
-1,0)上单调递减,
要存在实数b∈(1,2),使得当x∈(-1,b]时,函数f(x)的最大值为f(b),
则f(
-1)<f(1),代入化简得ln2a+
+ln2-1>0 (*)
令g(a)=ln2a+
+ln2-1(a>
),因g′(a)=
(1-
)>0恒成立,
故恒有g(a)>g(
)=ln2-
>0,∴a>
时,(*)式恒成立.
综上,实数a的取值范围是(1-ln2,+∞).
| 1 |
| 4 |
| 1 |
| 4 |
则f′(x)=
| 1 |
| x+1 |
| 1 |
| 2 |
| x(x-1) |
| 2(x+1) |
∴函数在(-1,0),(1,+∞)上单调递增,在(0,1)上单调递减,且f(0)=0,f(1)=ln2-
| 3 |
| 4 |
∴函数y=f(x)在x=1处取到极小值为ln2-
| 3 |
| 4 |
(Ⅱ)由题意f′(x)=
| x(2ax-(1-2a)) |
| x+1 |
(1)当a≤0时,函数f(x)在(-1,0)上单调递增,在(0,+∞)上单调递减,
此时,不存在实数b∈(1,2)使得当x∈(-1,b]时,函数f(x)的最大值为f(b);
(2)当a>0时,令f′(x)=0,有x=0或x=
| 1 |
| 2a |
①当a=
| 1 |
| 2 |
②当
| 1 |
| 2a |
| 1 |
| 2 |
| 1 |
| 2a |
| 1 |
| 2a |
此时由题,只需f(1)>0,解得a>1-ln2,又1-ln2<
| 1 |
| 2 |
∴此时实数a的取值范围是1-ln2<a<
| 1 |
| 2 |
③当
| 1 |
| 2a |
| 1 |
| 2 |
| 1 |
| 2a |
| 1 |
| 2a |
要存在实数b∈(1,2),使得当x∈(-1,b]时,函数f(x)的最大值为f(b),
则f(
| 1 |
| 2a |
| 1 |
| 4a |
令g(a)=ln2a+
| 1 |
| 4a |
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| 4a |
故恒有g(a)>g(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
综上,实数a的取值范围是(1-ln2,+∞).
点评:本题主要运用了分类讨论的方法,由条件逐层分析,逐步确定分类条件,一步一步讨论,直至将问题解决,在用分类讨论的方法解决问题时,要记住做到“不重不漏”.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
已知a,b∈R,则下列命题正确的是( )
| A、若a>b,则a2>b2 |
| B、若|a|>b,则a2>b2 |
| C、若a>|b|,则a2>b2 |
| D、若a≠|b|,则a2≠b2 |
 一个几何体的三视图如图所示,则该几何体的体积是( )
一个几何体的三视图如图所示,则该几何体的体积是( )| A、π | B、2π | C、3π | D、4π |
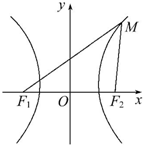 如图,设有双曲线
如图,设有双曲线