题目内容
11.已知数列{an}的前n项和为Sn,a1≠0,常数λ>0,且λa1an=S1+Sn对一切正整数n都成立.(1)求数列{an}的通项公式;
(2)设a1>0,λ=100,当n为何值时,数列$\{lg\frac{1}{a_n}\}$的前n项和最大?
分析 (1)利用递推关系即可得出.
(2)利用对数的运算性质、等差数列的通项公式与单调性即可得出.
解答 解:(1)令n=1,得$λa_1^2=2{S_1}=2{a_1},{a_1}(λ{a_1}-2)=0$,因为a1≠0,所以${a_1}=\frac{2}{λ}$,当n≥2时,$2{a_n}=\frac{2}{λ}+{S_n}$,$2{a_{n-1}}=\frac{2}{λ}+{S_{n-1}}$,两式相减得2an-2an-1=an(n≥2),
所以an=2an-1(n≥2),从而数列{an}为等比数列,
所以${a_n}={a_1}•{2^{n-1}}=\frac{2^n}{λ}$.
(2)当a1>0,λ=100时,由(1)知,an=$\frac{{2}^{n}}{100}$,
bn=lg$\frac{1}{{a}_{n}}$=$lg\frac{100}{{2}^{n}}$=2-nlg2.
所以数列{bn}是单调递减的等差数列,公差为-lg2,所以${b_1}>{b_2}>…>{b_6}=lg\frac{100}{2^6}=lg\frac{100}{64}>lg1=0$,
当n≥7时,${b_n}≤{b_7}=lg\frac{100}{2^7}<lg1=0$,所以数列$\{lg\frac{1}{a_n}\}$的前6项和最大.
点评 本题考查了等差数列的通项公式、数列递推关系、数列的单调性、对数的运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
4.在二维条形图中,两个比值相差越大,要推断的论述成立的可能性就越大.( )
| A. | $\frac{a}{a+b}$与$\frac{c}{c+d}$ | B. | $\frac{a}{c+d}$与$\frac{c}{a+b}$ | C. | $\frac{a}{a+b}$与$\frac{c}{b+c}$ | D. | $\frac{a}{b+d}$与$\frac{c}{a+c}$ |
20.已知A={α|α=k×45°+15°,k∈Z},当k=k0(k0∈Z)时,A中的一个元素与角-255°终边相同,若k0取值的最小正数为a,最大负数为b,则a+b=( )
| A. | -12 | B. | -10 | C. | -4 | D. | 4 |
20.点(-1,-1)在圆(x+a)2+(y-a)2=4的内部,则a的取值范围是( )
| A. | -1<a<1 | B. | 0<a<1 | C. | a<-1或a>1 | D. | a=±1 |
20.全世界越来越关注环境保护问题,某监测站点于2016年8月某日起连续n天监测空气质量指数(AQI),数据统计如下:
(1)根据所给统计表和频率分布直方图中的信息求出n,m的值,并完成頻率分布直方图:
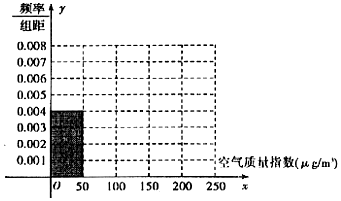
(2)由頻率分布直方图,求该组数据的平均数与中位数;
(3)在空气质量指数分别为51-100和151-200的监测数据中,用分层抽样的方法抽取5天,从中任意选取2天,求事件A“两天空气都为良”发生的概率.
| 空气质量指数(μg/m3) | 0-50 | 51-100 | 101-150 | 151-200 | 201-250 |
| 空气质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
| 天数 | 20 | 40 | m | 10 | 5 |

(2)由頻率分布直方图,求该组数据的平均数与中位数;
(3)在空气质量指数分别为51-100和151-200的监测数据中,用分层抽样的方法抽取5天,从中任意选取2天,求事件A“两天空气都为良”发生的概率.