题目内容
20.全世界越来越关注环境保护问题,某监测站点于2016年8月某日起连续n天监测空气质量指数(AQI),数据统计如下:| 空气质量指数(μg/m3) | 0-50 | 51-100 | 101-150 | 151-200 | 201-250 |
| 空气质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
| 天数 | 20 | 40 | m | 10 | 5 |
(2)由頻率分布直方图,求该组数据的平均数与中位数;
(3)在空气质量指数分别为51-100和151-200的监测数据中,用分层抽样的方法抽取5天,从中任意选取2天,求事件A“两天空气都为良”发生的概率.
分析 解:(1)由$0.004×50=\frac{20}{n}$,求出n=100,从而求出m=25,由此能完成频率分布直方图.
(2)由频率分布直方图能求出该组数据的平均数与中位数.
(3)在空气质量指数为51-100和151-200的监测天数中分别抽取4天和1天,在所抽収的5天中,将空气质量指数为51-100的4天分别记为a,b,c,d;将空气质量指数为151-200的1天记为e,利用列举法求出从中任取2天的基本事件和事件A“两天空气都为良”包含的基本事件,由此能求出事件A“两天都为良”发生的概率.
解答 解:(1)∵$0.004×50=\frac{20}{n}$,∴n=100,
∵20+40+m+10+5=100,∴m=25,
$\frac{40}{100×50}=0.008;\frac{25}{100×50}=0.005;\frac{10}{100×50}=0.002;\frac{5}{100×50}=0.001$.
由此完成频率分布直方图,如下图: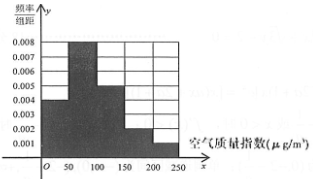
(2)由频率分布直方图得该组数据的平均数为:
$\overline{x}$=25×0.004×50+75×0.008×50+125×0.005×50+175×0.002×50+225×0.001×50=95,
∵[0,50)的频率为0.004×50=0.2,[50,100)的频率为:0.008×50=0.4,
∴中位数为:50+$\frac{0.5-0.2}{0.4}×50$=87.5.
(3)在空气质量指数为51-100和151-200的监测天数中分别抽取4天和1天,
在所抽収的5天中,将空气质量指数为51-100的4天分别记为a,b,c,d;
将空气质量指数为151-200的1天记为e,
从中任取2天的基本事件分别为:
(a,b),(a,c),(a,d),(a,e),(b,c),(b,d),
(b,e),(c,d),(c,e),(d,e)共10种,
其中事件A“两天空气都为良”包含的基本事件为:
(a,b),(a,c),(a,d),(b,c),(b,d),(c,d)共6种,
所以事件A“两天都为良”发生的概率是$P(A)=\frac{6}{10}=\frac{3}{5}$.
点评 本题考查频率分布直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案| P(K2≥k) | 0.10 | 0.05 | 0.025 |
| k | 2.706 | 3.841 | 5.024 |
| A. | 有97.5%以上的把握认为“爱好该项运动与性别有关” | |
| B. | 有97.5%以上的把握认为“爱好该项运动与性别无关” | |
| C. | 在犯错误的概率不超过5%的前提下,认为“爱好该项运动与性别有关” | |
| D. | 在犯错误的概率不超过5%的前提下,认为“爱好该项运动与性别无关” |
(1)若曲线y=f(x)在点(1,f(1))处的切线与直线x+y+1=0垂直,求a的值;
(2)讨论方程f(x)=1的实根的情况.
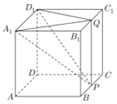 如图,正方体ABCD-A1B1C1D1中,AB=4,P、Q分别是棱BC与B1C1的中点.
如图,正方体ABCD-A1B1C1D1中,AB=4,P、Q分别是棱BC与B1C1的中点.
 则
则 ( )
( )