题目内容
对于函数f(x)和g(x),设α∈{x∈R|f(x)=0},β∈{x∈R|g(x)=0},若存在α,β,使得|α-β|≤1,则称f(x)与g(x)互为“零点关联函数”.若函数f(x)=ex-1+x-2与g(x)=x2-ax-a+3互为“零点关联函数”,则实数a的取值范围为 .
考点:函数的零点与方程根的关系
专题:函数的性质及应用
分析:先得出函数f(x)=ex-1+x-2的零点为x=1.再设g(x)=x2-ax-a+3的零点为β,根据函数f(x)=ex-1+x-2与g(x)=x2-ax-a+3互为“零点关联函数”,及新定义的零点关联函数,有|1-β|≤1,从而得出g(x)=x2-ax-a+3的零点所在的范围,最后利用数形结合法求解即可.
解答:
 解:函数f(x)=ex-1+x-2的零点为x=1.
解:函数f(x)=ex-1+x-2的零点为x=1.
设g(x)=x2-ax-a+3的零点为β,
若函数f(x)=ex-1+x-2与g(x)=x2-ax-a+3互为“零点关联函数”,
根据零点关联函数,则|1-β|≤1,
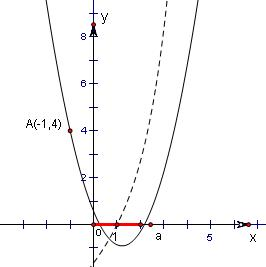
∴0≤β≤2,如图.
由于g(x)=x2-ax-a+3必过点A(-1,4),
故要使其零点在区间[0,2]上,则
,
即
解得2≤a≤3,
故答案为:[2,3].
 解:函数f(x)=ex-1+x-2的零点为x=1.
解:函数f(x)=ex-1+x-2的零点为x=1.设g(x)=x2-ax-a+3的零点为β,
若函数f(x)=ex-1+x-2与g(x)=x2-ax-a+3互为“零点关联函数”,
根据零点关联函数,则|1-β|≤1,
∴0≤β≤2,如图.
由于g(x)=x2-ax-a+3必过点A(-1,4),
故要使其零点在区间[0,2]上,则
|
即
|
解得2≤a≤3,
故答案为:[2,3].
点评:本题主要考查了函数的零点,考查了新定义,主要采用了转化为判断函数的图象的零点的取值范围问题,解题中注意体会数形结合思想与转化思想在解题中的应用

练习册系列答案
相关题目
已知某企业上半年前5个月产品广告投入与利润额统计如下:
由此所得回归方程为y=7.5x+a,若6月份广告投入10(万元)估计所获利润为( )
| 月份 | 1 | 2 | 3 | 4 | 5 |
| 广告投入(x万元) | 9.5 | 9.3 | 9.1 | 8.9 | 9.7 |
| 利润(y万元) | 92 | 89 | 89 | 87 | 93 |
| A、95.25万元 |
| B、96.5万元 |
| C、97万元 |
| D、97.25万元 |
